1. Thiết diện của một hình
Định nghĩa: Thiết diện (hay mặt cắt) của hình \(H\) khi cắt bởi mặt phẳng \(\left( P \right)\) là phần chung của \(mp\left( P \right)\) và hình \(H\).
Ví dụ:
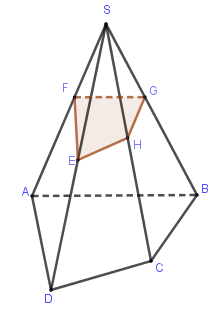
Mặt phẳng \(\left( \alpha \right)\) cắt các mặt phẳng \(\left( {SAB} \right),\left( {SBC} \right),\left( {SCD} \right),\left( {SDA} \right)\) lần lượt theo các giao tuyến \(FG,GH,HE,EF\).
Khi đó, thiết diện của hình chóp \(S.ABCD\) khi cắt bởi \(\left( \alpha \right)\) chính là tứ giác \(FGHE\).
2. Phương pháp xác định thiết diện của hình chóp
Cho hình chóp \(S.{A_1}{A_2}...{A_n}\), cắt hình chóp bởi một mặt phẳng \(\left( \alpha \right)\). Xác định thiết diện của hình chóp khi cắt bở mặt phẳng \(\left( \alpha \right)\).
Phương pháp:
- Bước 1: Tìm giao điểm của mặt phẳng \(\left( \alpha \right)\) với các đường thẳng chứa các cạnh của hình chóp.
- Bước 2: Nối các giao điểm tìm được ở trên thành đa giác.
- Bước 3: Kết luận: Đa giác tìm được ở trên chính là thiết diện của hình chóp khi cắt bởi mặt phẳng \(\left( \alpha \right)\).
- Giao điểm ở bước 1 thường được tìm bằng cách:
+) Tìm hai đường thẳng \(a,b\) lần lượt thuộc các mặt phẳng \(\left( \alpha \right),\left( \beta \right)\), đồng thời chúng nằm trong mặt phẳng \(\left( \gamma \right)\) nào đó.
+) Giao điểm \(M = a \cap b\) chính là điểm chung của \(\left( \alpha \right)\) và \(\left( \beta \right)\).
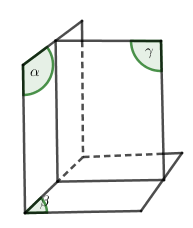
- Đường thẳng chứa cạnh của thiết diện chính là giao tuyến của mặt phẳng \(\left( \alpha \right)\) với mỗi mặt của hình chóp.
Ví dụ: Cho hình chóp \(S.ABCD\) có \(ABCD\) là tứ giác lồi và một điểm \(M\) nằm trên cạnh \(SB\). Xác định thiết diện cắt bởi mặt phẳng \(\left( {ADM} \right)\) với hình chóp.
Giải:
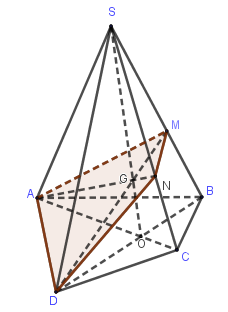
Trước hết ta sẽ tìm điểm $N$ là giao điểm của $(ADM)$ với $SC$.
Trong mặt phẳng \(\left( {ABCD} \right)\), gọi \(O = AC \cap BD \Rightarrow SO \subset \left( {SBD} \right)\).
Trong mặt phẳng \(\left( {SBD} \right)\), gọi \(G = SO \cap DM \Rightarrow G \in SO \subset \left( {SAC} \right)\).
Trong mặt phẳng \(\left( {SAC} \right)\), gọi \(N = AG \cap SC\).
Ta có:
+ $(ADM)$ cắt $(SAB)$ theo giao tuyến $AM$.
+ $(ADM)$ cắt $(SAD)$ theo giao tuyến $AD$.
+ $(ADM)$ cắt $(SCD)$ theo giao tuyến $DN$.
+ $(ADM)$ cắt $(SBC)$ theo giao tuyến $MN$.
Thiết diện cần tìm là tứ giác \(ADNM\).

