Đề bài
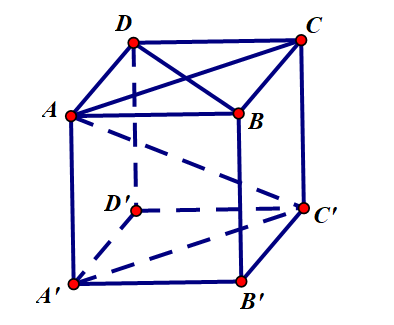
Cho hình lập phương ABCD.A′B′C′D′
a) Hãy phân tích các vecto →AC′;→BD theo ba vecto →AB;→AD;→AA′
b) Tính cos (→AC′;→BD) và từ đó suy ra →AC′;→BD vuông góc với nhau
Video hướng dẫn giải
Lời giải chi tiết
a)→AC′=→AC+→AA′=→AB+→AD+→AA′→BD=→AD−→ABb)cos(→AC′,→BD)=→AC′.→BD|→AC′|.|→BD|→AC′.→BD=(→AB+→AD+→AA′).(→AD−→AB)=(→AB+→AD+→AA′).→AD−(→AB+→AD+→AA′).→AB=→AB.→AD+→AD.→AD+→AA′.→AD−→AB.→AB−→AD.→AB−→AA′.→AB(1)
Hình lập phương ABCD.A′B′C′D′ nên AB,AD,AA′ đôi một vuông góc với nhau
(1)=→0+→AD2+→0−→AB2−→0−→0=0(AB=AD)⇒cos(→AC′,→BD)=→AC′.→BD|→AC′|.|→BD|=0⇒(→AC′,→BD)=900
Vậy hai vecto trên vuông góc với nhau.