Đề bài
Cho bốn điểm \(A,B,C\) và \(D\) không đồng phẳng. Gọi \(M,N\) lần lượt là trung điểm của \(AC\) và \(BC\). Trên đoạn \(BD\) lấy điểm \(P\) sao cho \(BP=2PD\).
a) Tìm giao điểm của đường thẳng \(CD\) và mặt phẳng \((MNP)\).
b) Tìm giao tuyến của hai mặt phẳng \((MNP)\) và \((ACD)\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Tìm giao điểm của \(CD\) và một đường thẳng bất kì nằm trong mặt phẳng \((MNP)\). Chú ý kiểm tra các đường thẳng sẵn có như \(MN,NP,PM\) trước.
b) Tìm hai điểm chung của hai mặt phẳng \((MNP)\) và \((ACD)\).
Lời giải chi tiết
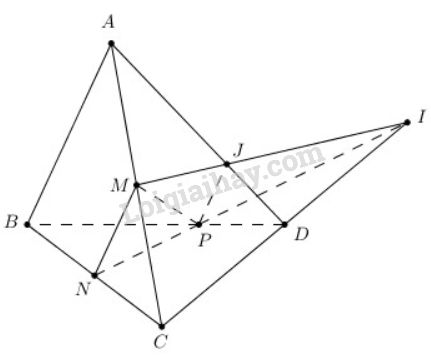
a) Ta có: \(\dfrac{{BN}}{{BC}} = \dfrac{1}{2},\dfrac{{BP}}{{BD}} = \dfrac{2}{3} \Rightarrow \dfrac{{BN}}{{BC}} \ne \dfrac{{BP}}{{BD}}\) nên \(NP\) không song song \(CD.\)
Trong \((BCD)\), gọi \(I\) là giao điểm của \(NP\) và \(CD\) \( \Rightarrow I \in CD\).
\(I\in NP\subset (MNP) \Rightarrow I \in \left( {MNP} \right)\).
Vậy \(CD\cap (MNP)=I\).
b) Trong \((ACD)\), gọi \(J=MI\cap AD\)
\(J\in AD\subset (ACD)\), \(M\in AC\subset (ACD) \Rightarrow MJ \subset \left( {ACD} \right)\).
Mà \(J \in MI \subset \left( {MNP} \right)\) \( \Rightarrow J \in \left( {MNP} \right)\) \( \Rightarrow MJ \subset \left( {MNP} \right)\).
Vậy \((MNP)\cap(ACD)=MJ\).

