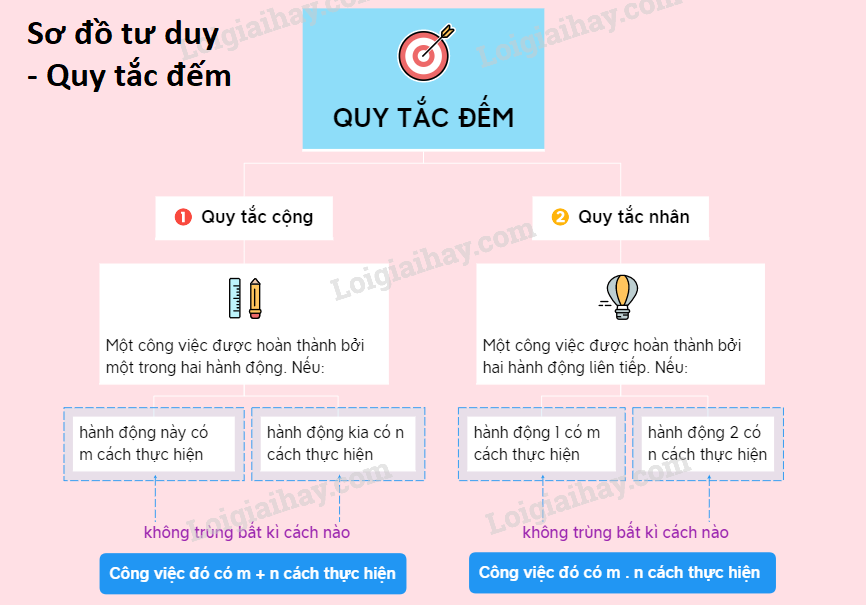
1. Quy tắc cộng
Quy tắc:
Có \(k\) phương án \({A_1},{A_2},{A_3},...,{A_k}\) để thực hiện công việc. Trong đó:
- Có \({n_1}\) cách thực hiện phương án \({A_1}\),
- Có \({n_2}\) cách thực hiện phương án \({A_2}\)
…
- Có \({n_k}\) cách thực hiện phương án \({A_k}\).
Khi đó, số cách để thực hiện công việc là: \({n_1} + {n_2} + ... + {n_k}\) cách.
Nếu \(A\) và \(B\) là hai tập hợp hữu hạn không giao nhau thì số phần tử của \(A \cup B\) bằng tổng số phần tử của \(A\) và của \(B\), tức là: \(\left| {A \cup B} \right| = \left| A \right| + \left| B \right|\).
Ví dụ: Đi từ Hà Nội vào TP. Hồ Chí Minh có thể đi bằng ô tô, tàu hỏa, máy bay. Biết có \(10\) chuyến ô tô, \(2\) chuyến tàu hỏa và \(1\) chuyến máy bay có thể vào được TP. Hồ Chí Minh. Số cách có thể đi để vào TP. Hồ Chí Minh từ Hà Nội là:
Hướng dẫn:
Có \(3\) phương án đi từ Hà Nội vào TP. Hồ Chí Minh là: ô tô, tàu hỏa, máy bay.
- Có \(10\) cách đi bằng ô tô (vì có \(10\) chuyến).
- Có \(2\) cách đi bằng tàu hỏa (vì có \(2\) chuyến).
- Có \(1\) cách đi bằng máy bay (vì có \(1\) chuyến).
Vậy có tất cả \(10 + 2 + 1 = 13\) cách đi từ HN và TP.HCM.
2. Quy tắc nhân
Có \(k\) công đoạn \({A_1},{A_2},...,{A_k}\) để thực hiện công việc.
- Có \({n_1}\) cách thực hiện công đoạn \({A_1}\).
- Có \({n_2}\) cách thực hiện công đoạn \({A_2}\).
…
- Có \({n_k}\) cách thực hiện công đoạn \({A_k}\).
Khi đó, số cách để thực hiện công việc là: \({n_1}.{n_2}.....{n_k}\) cách.
Ví dụ: Mai muốn đặt mật khẩu nhà có \(4\) chữ số. Chữ số đầu tiên là một trong \(3\) chữ số \(1;2;0\), chữ số thứ hai là một trong \(3\) chữ số \(6;4;3\), chữ số thứ ba là một trong \(4\) chữ số \(9;1;4;6\) và chữ số thứ tư là một trong \(4\) chữ số \(8;6;5;4\). Có bao nhiêu cách để Mai đặt mật khẩu nhà?
Hướng dẫn:
Việc đặt mật khẩu nhà có \(4\) công đoạn (từ chữ số đầu tiên đến chữ số cuối cùng).
- Có \(3\) cách thực hiện công đoạn 1 (ứng với \(3\) cách chọn chữ số đầu tiên).
- Có \(3\) cách thực hiện công đoạn 2 (ứng với \(3\) cách chọn chữ số thứ hai).
- Có \(4\) cách thực hiện công đoạn 3 (ứng với \(4\) cách chọn chữ số thứ ba).
- Có \(4\) cách thực hiện công đoạn 4 (ứng với \(4\) cách chọn chữ số thứ tư).
Vậy có tất cả \(3.3.4.4 = 144\) cách để Mai đặt mật khẩu nhà.