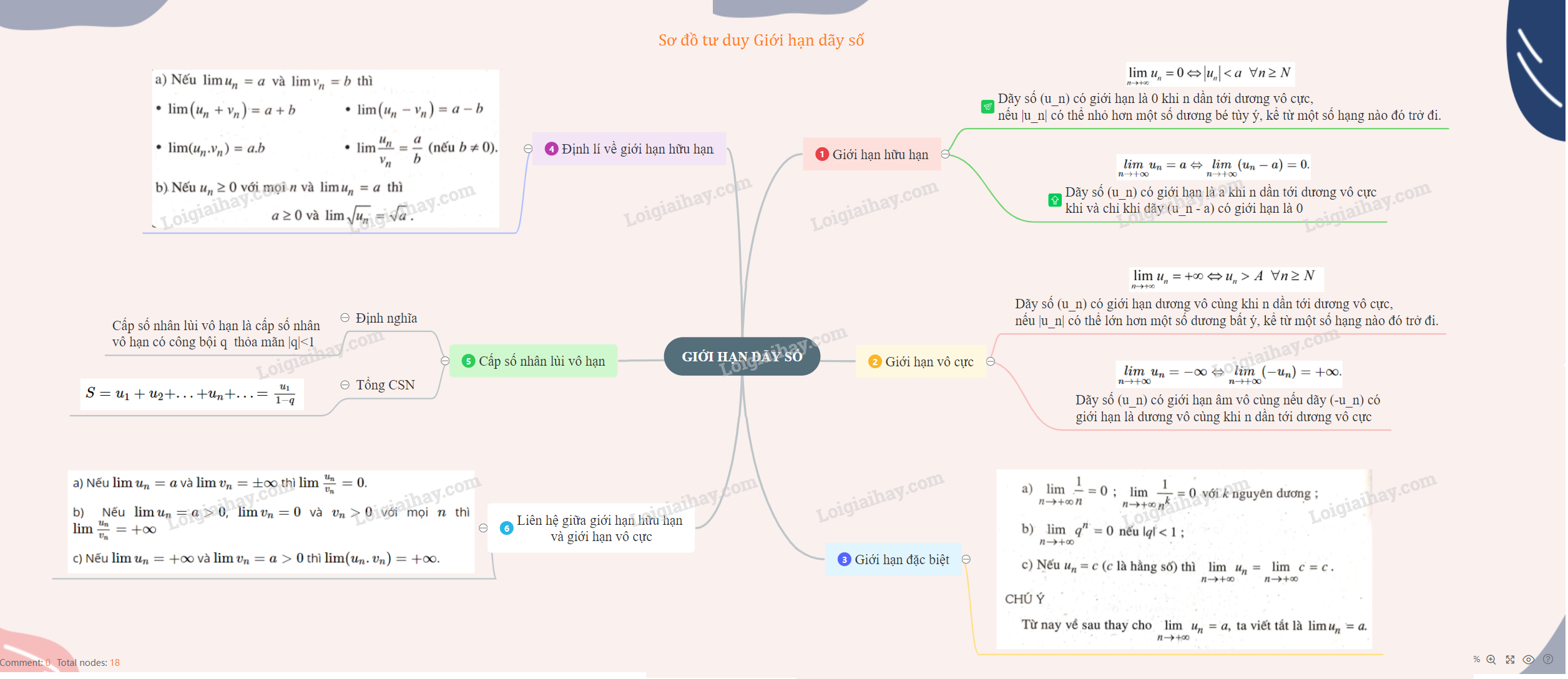
1. Giới hạn hữu hạn
+) limn→+∞un=0 khi và chỉ khi |un| có thể nhỏ hơn một số dương bé tùy ý, kể từ một số hạng nào đó trở đi.
+) limn→+∞un=a⇔limn→+∞(un−a)=0.
2. Giới hạn vô cực
+) limn→+∞un=+∞ khi và chỉ khi un có thể lớn hơn một số dương tùy ý, kể từ một số hạng nào đó trở đi.
+ limn→+∞un=−∞⇔limn→+∞(−un)=+∞.
3. Các giới hạn đặc biệt
a) lim;
\lim \frac{1}{n^{k}} = 0;
\lim n^k= +∞, với k nguyên dương.
b) \lim q^n= 0 nếu |q| < 1;
\lim q^n= +∞ nếu q > 1.
c) \lim c = c (c là hằng số).
4. Định lí về giới hạn hữu hạn
a) Nếu \lim u_n=a và \lim v_n= b, thì:
lim\left( {{u_{n}}+{v_n}} \right)= a +b
lim{\rm{ }}({u_n} - {v_n}){\rm{ }} = {\rm{ }}a - b
lim{\rm{ }}({u_n}.{v_n}) = ab
lim{{{u_n}} \over {{v_n}}} = {a \over b} (nếu b ≠ 0).
b) Nếu u_n≥ 0 với mọi n và lim u_n= a thì a > 0 và lim \sqrt{u_n}= \sqrt a.
5. Định lí liên hệ giữa giới hạn hữu hạn và giới hạn vô cực.
a) Nếu \lim u_n=a và \lim v_n= ± ∞ thì \lim \frac{u_{n}}{v_{n}}= 0.
b) Nếu \lim u_n=a > 0, \lim v_n= 0 và v_n> 0 với mọi n thì \lim \frac{u_{n}}{v_{n}} = +∞
c) Nếu \lim u_n= +∞ và \lim v_n= a > 0 thì \lim (u_n.v_n) = +∞.
6. Cấp số nhân lùi vô hạn
+ Cấp số nhân lùi vô hạn là cấp số nhân vô hạn có công bội q thỏa mãn |q| <1.
+) Công thức tính tổng S của cấp số lùi vô hạn (u_n):
S = {u_1} + {u_2} + ... + {u_n} + ... = {{{u_1}} \over {1 - q}}