Video hướng dẫn giải
Cho hàm số \(y = \cos 2x\)
LG a
Chứng minh rằng: \(\cos 2(x + k π) = \cos 2x\) với mọi số nguyên \(k\). Từ đó vẽ đồ thị (C) của hàm số \(y = \cos2x\).
Phương pháp giải:
Sử dụng chu kì tuần hoàn của hàm số cos
Lời giải chi tiết:
Ta có: \(\cos 2(x + k π) = \cos (2x + k2 π) = \cos 2x\).
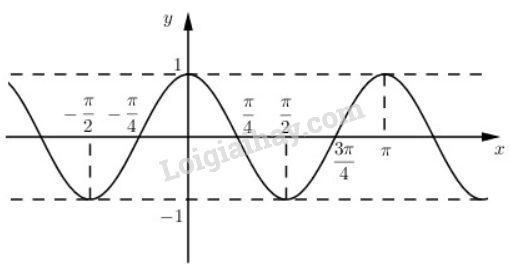
_ Từ kết quả trên ta suy ra hàm số \(y = \cos 2x\) là hàm số tuần hoàn có chu kì là \(π\).
_ Do đó, ta chỉ cần vẽ đồ thị hàm số \(y = \cos 2x\) trên \([0, π]\) và tịnh tiến nó song song với trục \(Ox\) các đoạn có độ dài là \(π\).
Bảng giá trị đặc biệt
| \(x\) | \(0\) | \({\pi \over 4}\) | \({\pi \over 2}\) | \({{3\pi } \over 4}\) | \(π\) |
| \(\cos 2x\) | \(1\) | \(0\) | \(-1\) | \(0\) | \(1\) |
Đồ thị hàm số :
LG b
Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ \(x = {\pi \over 3}\)
Phương pháp giải:
Phương trình tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm có hoành độ \(x=x_0\) là: \(y - {y_0} = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right)\)
Lời giải chi tiết:
Ta có: \({x_0} = {\pi \over 3} \Rightarrow {y_0} = \cos {{2\pi } \over 3} = - {1 \over 2}\)
Ta lại có:
\(\eqalign{
& f'(x) = - 2\sin 2x \cr
& \Rightarrow f'({\pi \over 3}) = - 2\sin {{2\pi } \over 3} = - \sqrt 3 \cr} \)
Vậy phương trình tiếp tuyến cần tìm là:
\(y + {1 \over 2} = - \sqrt 3 (x - {\pi \over 3}) \Leftrightarrow y = - \sqrt 3 x + {{\pi \sqrt 3 } \over 3} - {1 \over 2}\)
LG c
Tìm tập xác định của hàm số \(z = \sqrt {{{1 - \cos 2x} \over {1 + {{\cos }^2}2x}}} \)
Phương pháp giải:
Hàm số \(y = \sqrt {f\left( x \right)} \) xác định \( \Leftrightarrow f\left( x \right) \ge 0\), sử dụng tính chất \(\cos \alpha \in \left[ { - 1;1} \right]\).
Lời giải chi tiết:
Ta có:
\(|cos 2x| ≤ 1\) nên \(1 – cos 2x ≥ 0 ,∀ x ∈ \mathbb R\).
\( \Rightarrow \dfrac{{1 - \cos 2x}}{{1 + {{\cos }^2}2x}} \ge 0\,\,\forall x \in R\)
Do đó, tập xác định của hàm số \(z\) là \(\mathbb R\).

