Đề bài
Gọi MM là giao điểm của đường thẳng dd và mặt phẳng (α)(α). Chứng minh MM là điểm chung của (α)(α) với một mặt phẳng bất kì chứa dd
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Gọi (β)(β) là mặt phẳng bất kì chứa dd, chứng minh {M∈(α)M∈(β)
Lời giải chi tiết
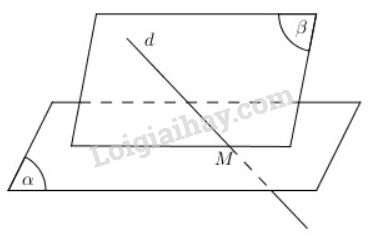
M=d∩(α)⇒M∈(α)
Gọi (β) là mặt phẳng bất kì chứa d, ta có {M∈dd⊂(β)⇒M∈(β)
Vậy M là điểm chung của (α) và mọi mặt phẳng (β) chứa d.

