Video hướng dẫn giải
Tính:
LG a
limx→+∞(x4−x2+x−1)
Phương pháp giải:
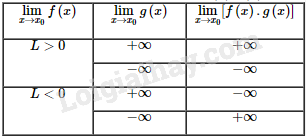
Sử dụng quy tắc tìm giới hạn của tích f(x).g(x).Lời giải chi tiết:
limx→+∞(x4−x2+x−1)=limx→+∞x4(1−1x2+1x3−1x4)limx→+∞x4=+∞limx→+∞(1−1x2+1x3−1x4)=1>0⇒limx→+∞(x4−x2+x−1)=+∞
LG b
limx→−∞(−2x3+3x2−5)
Lời giải chi tiết:
limx→−∞(−2x3+3x2−5)=limx→−∞x3(−2+3x−5x2)limx→−∞x3=−∞;limx→−∞(−2+3x−5x2)=−2<0⇒limx→−∞x3(−2+3x−5x2)=+∞
LG c
limx→−∞(√x2−2x+5)
Lời giải chi tiết:
limx→−∞(√x2−2x+5)=limx→−∞√x2(1−2x+5x2)=limx→−∞|x|√1−2x+5x2=limx→−∞[−x√1−2x+5x2]limx→−∞(−x)=+∞limx→−∞(√1−2x+5x2)=1>0⇒limx→−∞(√x2−2x+5)=+∞
LG d
limx→+∞√x2+1+x5−2x
Lời giải chi tiết:
limx→+∞√x2+1+x5−2x=limx→+∞√x2(1+1x2)+x5−2x=limx→+∞|x|√1+1x2+x5−2x=limx→+∞x√1+1x2+x5−2x=limx→+∞x(√1+1x2+1)x(5x−2)=limx→+∞√1+1x2+15x−2=1+1−2=−1