Đề bài
Chứng minh rằng: Nếu một phép dời hình biến tam giác ABC thành tam giác A′B′C′ thì nó cũng biến trọng tâm của tam giác ABC tương ứng thành trọng tâm của tam giác A′B′C′
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Phép dời hình biến các đoạn thẳng thành các đoạn thẳng, do đó biến các trung tuyến thành các trung tuyến tương ứng.
Lời giải chi tiết
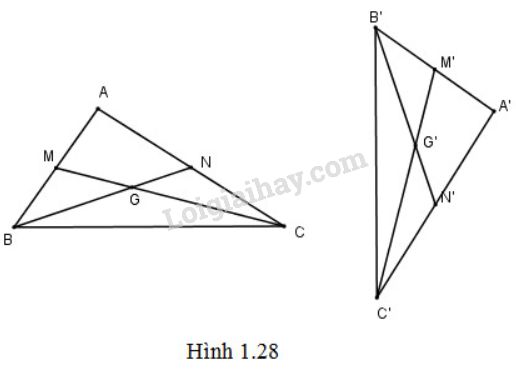
Gọi phép dời hình đó là f.
Gọi M, N là trung điểm của AB, AC, G là trọng tâm của tam giác ABC.
Do f biến AB,AC thành A′B′,A′C′ nên f biến M,N thành M′,N′ là trung điểm của của A′B′,A′C′.
Vậy f biến các trung tuyến CM,BN của tam giác ABC tương ứng thành các trung tuyến C′M′,B′N′ của tam giác A′B′C′.
Do đó f biến G là giao điểm của CM, BN thành G' là giao điểm của C'M', B'N' hay G' là trọng tâm tam giác A'B'C'.
Từ đó suy ra f biến trọng tâm G của tam giác ABC thành trọng tâm G′ của tam giác A′B′C′.
Cách khác:
Gọi f là phép dời hình biến tam giác ABC thành tam giác A’B’C’.
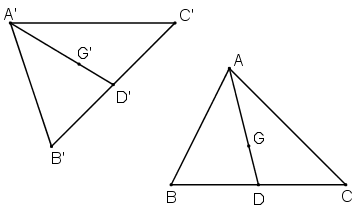
Gọi D là trung điểm của BC, D’ = f(D).
Gọi G là trọng tâm ΔABC, G’ = f(G).
+ B, D, C thẳng hàng ⇒ B’; D’; C’ thẳng hàng.
+ A; G; D thẳng hàng ⇒ A’; G’; D’ thẳng hàng.
+ B’D’ = BD = BC/2 = B’C’/2 ⇒ D’ là trung điểm B’C’.
+ A’G’ = AG = 2.AD/3 = 2.A’D’/3 ⇒ G’ là trọng tâm ΔA’B’C’.
Vậy phép dời hình f biến trọng tâm G của ΔABC thành trọng tâm G’ của ΔA’B’C’ (đpcm).

