Đề bài
Tứ diện ABCDABCD có hai mặt ABCABC và ADCADC nằm trong hai mặt phẳng vuông góc với nhau. Tam giác ABCABC vuông tại AA có AB=a,AC=bAB=a,AC=b. Tam giác ADCADC vuông tại DD có CD=aCD=a.
a) Chứng minh các tam giác BADBAD và BDCBDC đều là tam giác vuông
b) Gọi II và KK lần lượt là trung điểm của ADAD và BCBC. Chứng minh IKIK là đoạn vuông góc chung của hai đường thẳng ADAD và BCBC.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Chứng minh BA⊥(ACD);CD⊥(ABD)BA⊥(ACD);CD⊥(ABD).
b) Gọi J là trung điểm của AC, chứng minh AD⊥(IJK)⇒IK⊥ADAD⊥(IJK)⇒IK⊥AD.
Chứng minh tam giác IBCIBC cân tại I ⇒IK⊥BC⇒IK⊥BC.
Lời giải chi tiết
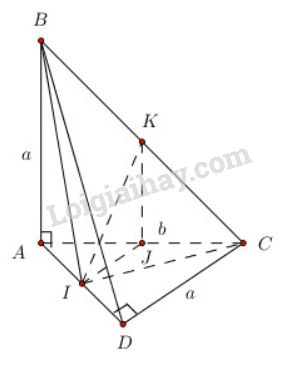
a)
{(ABC)⊥(ADC)(ABC)∩(ADC)=AC(ABC)⊃AB⊥AC⇒BA⊥(ADC)
⇒BA⊥AD⇒ΔBAD vuông tại A.
{BA⊥(ADC)⇒CD⊥BACD⊥AD⇒CD⊥(BAD)
⇒CD⊥DB⇒ΔBDC vuông tại D.
b) Gọi J là trung điểm của AC⇒KJ//BA (đường trung bình của ΔABC)
Mà BA⊥(ADC)⇒KJ⊥(ADC) ⇒KJ⊥AD (1)
Ta cũng có IJ//DC (đường trung bình của ΔADC )
Mà DC⊥AD ⇒IJ⊥AD (2)
Từ (1) và (2) suy ra: AD⊥(KIJ)⇒AD⊥IK(3)
Ta lại có: ΔBAI=ΔCDI(c.g.c)⇒IB=IC
⇒ΔBIC cân đỉnh I⇒IK⊥BC (4)
Từ (3) và (4) suy ra IK là đoạn vuông góc chung của AD và BC.

