Đề bài
Trong không gian cho hai vecto \(\overrightarrow a ;\,\overrightarrow b \) đều khác vecto – không.
Hãy xác định các vecto \(\overrightarrow m = 2\overrightarrow a ;\,\overrightarrow n = - 3\overrightarrow b ;\,\overrightarrow p = \overrightarrow m + \overrightarrow n \)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Vẽ các véc tơ \(\overrightarrow a ;\,\overrightarrow b \) bất kì.
- Chọn một điểm làm gốc, lần lượt dựng hai véc tơ \(\overrightarrow m ;\,\overrightarrow n \).
- Sử dụng quy tắc hình bình hành dựng véc tơ \(\overrightarrow p \).
Lời giải chi tiết
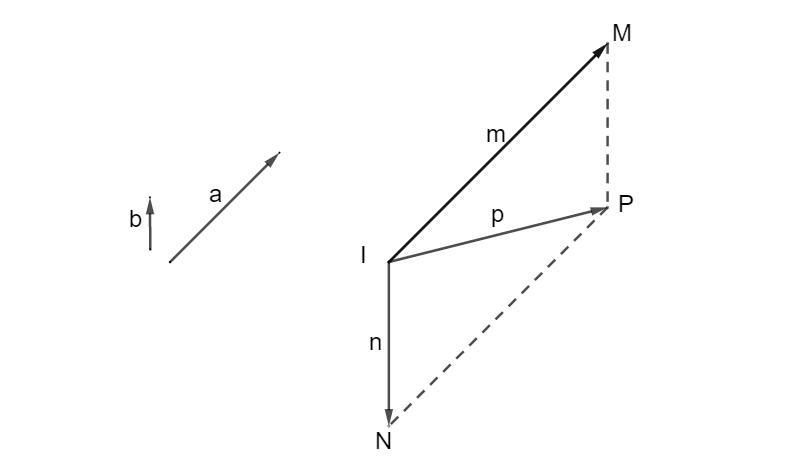
Lấy điểm \(I\) bất kì.
+) Vẽ \(\overrightarrow {IM} \) sao cho:
\(\left\{ \begin{array}{l}
IM = 2\left| {\overrightarrow a } \right|\\
IM\;//\;a\\
\overrightarrow a \,;\;\overrightarrow {IM} \text {cùng hướng}
\end{array} \right.\)
+) Vẽ \(\overrightarrow {IN} \) sao cho:
\(\left\{ \begin{array}{l}
IN =3 \left| {\overrightarrow b } \right|\\
IN\;//\;b\\
\overrightarrow b \,;\;\overrightarrow {IN} \text {ngược hướng}
\end{array} \right.\)
+) Vẽ hình bình hành \(IMPN\)
\( \Rightarrow \overrightarrow p = \overrightarrow {IP} \)