Đề bài
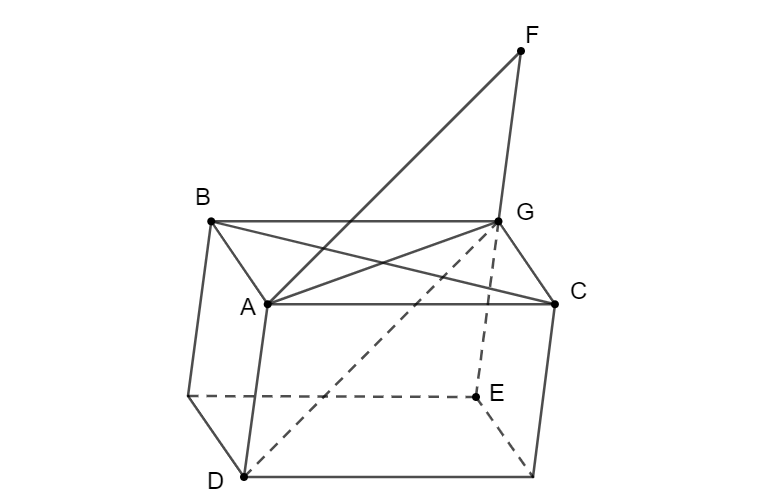
Cho hình tứ diện ABCDABCD. Hãy xác định hai điểm E,FE,F sao cho:
a) →AE=→AB+→AC+→AD;−−→AE=−−→AB+−−→AC+−−→AD;
b) →AF=→AB+→AC−→AD.−−→AF=−−→AB+−−→AC−−−→AD.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng quy tắc hình bình hành.
Lời giải chi tiết
a) Lấy điểm GG sao cho →AB+→AC=→AG−−→AB+−−→AC=−−→AG
⇒⇒ GG là đỉnh của hình bình hành ABGCABGC. Ta có:
→AB+→AC+→AD=→AE−−→AB+−−→AC+−−→AD=−−→AE ⇔→AG+→AD=→AE⇔−−→AG+−−→AD=−−→AE
⇒⇒ EE là đỉnh của hình bình hành ADEGADEG.
Hay AEAE là đường chéo của hình hộp có ba cạnh AB,AC,ADAB,AC,AD.
b) Ta có
→AB+→AC−→AD=→AF⇔→AG−→AD=→AF⇔→DG=→AF
⇒ F là đỉnh của hình bình hành ADGF.