Đề bài
Cho tam giác ABC vuông tại A,AH là đường cao kẻ từ A. Tìm một phép đồng dạng biến tam giác HBA thành tam giác ABC.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Thực hiện liên tiếp hai phép biến hình:
- Phép đối xứng qua đường thẳng d, với d là phân giác của góc B.
- Phép vị tự tâm B, tỉ số AC/AH.
Lời giải chi tiết
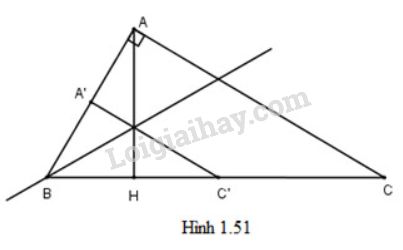
Gọi d là đường phân giác của ˆB.
Gọi A′=Dd(H),C′=Dd(A).
Dễ thấy A′∈AB,C′∈BC.
Ta có Dd biến ∆HBA thành ∆A′BC′.
Suy ra ∆HBA=∆A′BC′ nên góc A′=H=900
⇒C′A′//CA
Theo định lý Ta-let có BABA′=BCBC′=ACA′C′=ACAH=k
⇒→BA=k→BA′ ⇒V(B;k)(A′)=A
→BC=k→BC′⇒V(B;k)(C′)=C
Mà V(B;k)(B)=B nên V(B;k)(ΔA′BC′)=ΔABC.
Do đó phép đồng dạng có được bằng cách thực hiện liên tiếp Dd và V(B,k) sẽ biến △HBA thành △ABC

