Đề bài
Cho hình chóp S.ABCDS.ABCD có ABAB và CDCD không song song. Gọi MM là một điểm thuộc miền trong của tam giác SCDSCD.
a) Tìm giao điểm NN của đường thẳng CDCD và mặt phẳng (SBM)(SBM).
b) Tìm giao tuyến của hai mặt phẳng (SBM)(SBM) và (SAC)(SAC).
c) Tìm giao điểm II của đường thẳng BMBM và mặt phẳng (SAC)(SAC).
d) Tìm giao điểm PP của SCSC và mặt phẳng (ABM)(ABM), từ đó suy ra giao tuyến của hai mặt phẳng (SCD)(SCD) và (ABM)(ABM).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Kéo dài SMSM cắt CDCD tại NN.
b) Tìm hai điểm chung của hai mặt phẳng (SBM)(SBM) và (SAC)(SAC).
c) Tìm một đường thẳng nằm trong (SAC)(SAC) cắt BMBM tại II.
d) Tìm một đường thẳng nằm trong (ABM)(ABM) cắt SCSC tại PP. Xác định hai điểm chung của hai mặt phẳng (SCD)(SCD) và (ABM)(ABM).
Lời giải chi tiết
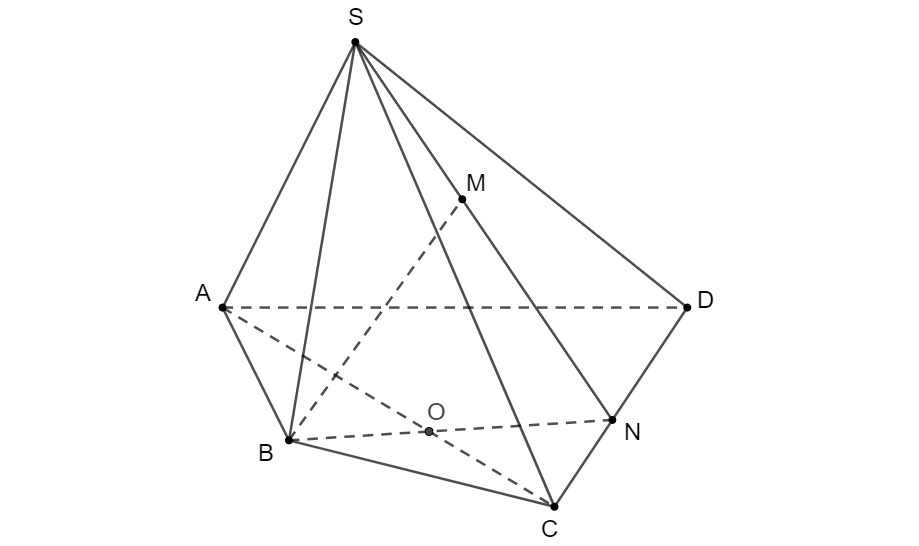
a) Trong (SCD)(SCD) kéo dài SMSM cắt CDCD tại NN.
⇒{N∈CDN∈SM⊂(SMB) ⇒N=CD∩(SBM)
b) (SBM)≡(SBN).
Dễ thấy S∈(SAC)∩(SBM).
Trong (ABCD) gọi O=AC∩BN
⇒{O∈AC⊂(SAC)O∈BN⊂(SBN) ⇒O∈(SAC)∩(SBN)
Do đó: SO=(SAC)∩(SBM).
c) Trong (SBN) gọi I là giao của MB và SO. Mà SO⊂(SAC)
Do đó: I=BM∩(SAC)
d) Trong (SAC), gọi P=AI∩SC
⇒{P∈AI⊂(ABM)P∈SC ⇒P=SC∩(ABM)
Lại có P∈SC, mà SC⊂(SCD)⇒P∈(SCD).
⇒P∈(AMB)∩(SCD).
Lại có: M∈(SCD) (gt)
⇒M∈(MAB)∩(SCD)
Vậy giao tuyến của (MAB) và (SCD) là đường thẳng MP.
Cách khác:
Câu d có thể dựng hình bằng cách khác như sau:
Trong (ABCD) , gọi K=AB∩CD. Khi đó (ABM)≡(AKM)
Trong (SCD), gọi P=MK∩SC. Lại có MK⊂(ABM).
Do đó: P=SC∩(ABM)
Trong (SDC) gọi Q=MK∩SD, MK⊂(ABM)⇒Q=SD∩(ABM).
⇒PQ⊂(ABM),PQ⊂(SCD)⇒PQ=(SCD)∩(ABM).

