Đề bài
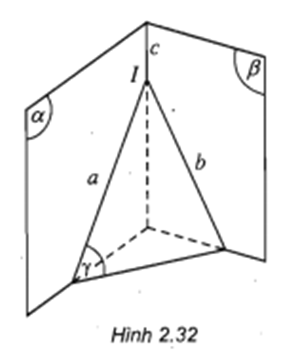
Cho hai mặt phẳng \((\alpha)\) và \((\beta)\). Một mặt phẳng \((\lambda)\) cắt \((\alpha)\) và \((\beta)\) lần lượt theo các giao tuyến \(a\) và \(b\). Chứng minh rằng khi \(a\) và \(b\) cắt nhau tại \(I\) thì \(I\) là điểm chung của \((\alpha)\) và \((\beta)\). (h.2.32).
Video hướng dẫn giải
Lời giải chi tiết
\(a\) và \(b\) cắt nhau tại \(I\) nên:
\(I \in a \subset (a)\) (vì \(a\) là giao tuyến của \((\alpha)\) và \((\lambda)\))
\(I \in b \subset (\beta )\) ( vì \(b\) là giao tuyến của \((\beta)\) và \((\lambda)\))
Nên \(I\) là điểm chung của \((\alpha)\) và \((\beta)\).