Đề bài
Trong không gian cho hai hình vuông ABCD và ABC′D′ có chung cạnh AB và nằm trong hai mặt phẳng khác nhau, lần lượt có tâm O và O′. Chứng minh rằng AB⊥OO′ và tứ giác CDD′C′ là hình chữ nhật.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Chứng minh →AB.→OO′=0, sử dụng công thức →a.→b=|→a|.|→b|.cos(→a;→b)
+) Chứng minh CDD'C' là tứ giác có một cặp cạnh đối song song và bằng nhau và có 1 góc vuông.
Lời giải chi tiết
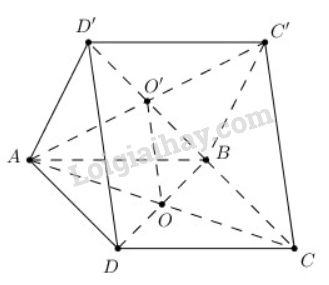
→AB.→OO′=→AB.(→AO′−→AO)
=→AB.→AO′−→AB.→AO
=AB.AO′.cos450−AB.AO.cos450
=0.
Vậy AB⊥OO′.
{CD//C′D′CD=C′D′⇒CDD′C′ là hình bình hành (Tứ giác có một cặp cạnh đối song song và bằng nhau).
Xét tam giác ACC′ có OO′ là đường trung bình của tam giác nên OO′//CC′.
Mà AB//CD và AB⊥OO′ nên CD⊥CC′.
⇒CDD′C′ là hình chữ nhật (Hình bình hành có 1 góc vuông).

