Đề bài
Cho tứ diện ABCDABCD. Gọi MM và NN lần lượt là trung điểm của các cạnh ABAB và CDCD trên cạnh ADAD lấy điểm PP không trùng với trung điểm của ADAD
a) Gọi EE là giao điểm của đường thẳng MPMP và đường thẳng BDBD. Tìm giao tuyến của hai mặt phẳng (PMN)(PMN) và (BCD)(BCD)
b) Tìm giao điểm của mặt phẳng (PMN)(PMN) và BCBC.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Muốn tìm giao tuyến của hai mặt phẳng, ta tìm hai điểm chung của hai mặt phẳng đó.
Lời giải chi tiết
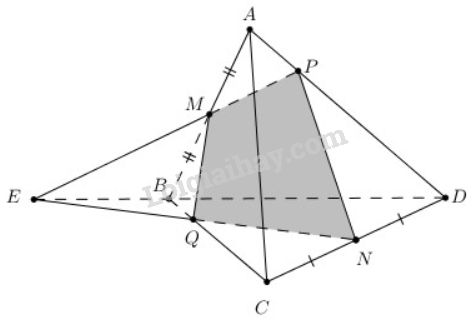
a) Trong (ABD)(ABD), ta có: E=MP∩BDE=MP∩BD. Vì:
{E∈BD⊂(BCD)⇒E∈(BCD)E∈MP⊂(MNP)⇒E∈(MNP)⇒E∈(BCD)∩(MNP)Lại có:{N∈CD⊂(BCD)⇒N∈(BCD)N∈(MNP)⇒N∈(BCD)∩(MNP)⇒NE=(BCD)∩(MNP) hay NE là giao tuyến của mặt phẳng BCD và MNP
b) Trong mặt phẳng (BCD) gọi Q là giao điểm của NE và BC ta có:
{Q∈BCQ∈NE⊂(MNP)⇒Q∈(MNP)⇒Q=BC∩(MNP)

