Đề bài
Câu 1: Cho ba mặt phẳng phân biệt (α),(β),(γ) có (α)∩(β)=d1; (β)∩(γ)=d2; (α)∩(γ)=d3. Khi đó ba đường thẳng d1,d2,d3:
A. Đôi một cắt nhau.
B. Đôi một song song.
C. Đồng quy.
D. Đôi một song song hoặc đồng quy.
Câu 2 : Trong không gian, cho 3 đường thẳng a,b,c, biết a∥b, a và c chéo nhau. Khi đó hai đường thẳng b và c:
A. Trùng nhau hoặc chéo nhau.
B. Cắt nhau hoặc chéo nhau.
C. Chéo nhau hoặc song song.
D. Song song hoặc trùng nhau.
Câu 3: Trong không gian, cho ba đường thẳng phân biệt a,b,c trong đó a∥b. Khẳng định nào sau đây sai?
A. Nếu a∥c thì b∥c.
B. Nếu c cắt a thì c cắt b.
C. Nếu A∈a và B∈b thì ba đường thẳng a,b,AB cùng ở trên một mặt phẳng.
D. Tồn tại duy nhất một mặt phẳng qua a và b.
Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I,J,E,F lần lượt là trung điểm SA,SB,SC,SD. Trong các đường thẳng sau, đường thẳng nào không song song với IJ?
A. EF. B. DC.
C. AD. D. AB.
Câu 5: Cho hình chóp S.ABCD có AB không song song với CD. Gọi A′,B′,C′,D′ lần lượt là trung điểm của các cạnh SA,SB,SC và SD. Trong các đường thẳng sau đây, đường thẳng nào song song với A′B′?
A. AC. B. CD.
C. C′D′. D. AB.
Câu 6: Kí hiệu nào sau đây là tên của mặt phẳng
A. a B. mpQ
C. (P) D. mpAB
Câu 7: Cho điểm A thuộc mặt phẳng (P), mệnh đề nào sau đây đúng :
A. A∈P B. A∈(P)
C. A⊂mp(P) D.A⊂mpP
Câu 8: Khi điểm M thuộc đường thẳng d, mệnh đề nào sau đây đúng :
A. M⊂d B. M∉d
C. M \in d \not\subset (P) \Rightarrow M \notin (P) D.M \in d
Câu 9: Cho đường thẳng a thuộc mặt phẳng (Q), khi đó mệnh đề nào sau đây sai ?
A. a \subset (Q)
B. M \in a \subset (Q) \Rightarrow M \subset (Q)
C. a \in mp(Q)
D. a và (Q) có vô số điểm chung
Lời giải chi tiết
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| D | B | B | C | D | C | B | D | C |
Câu 1: Chọn D.
Dựa vào định lý 1.
Câu 2: Chọn B
Câu 3: Chọn B.
c có thể chéo nhau vớib.
Câu 4: Chọn C.
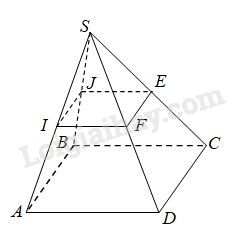
Ta có IJ là đường trung bình tam giác SAB nên IJ{\rm{//}}AB, nên D đúng.
ABCD là hình bình hành nên AB{\rm{//}}CD. Suy ra IJ{\rm{//}}CD. Nên B đúng.
EF là đường trung bình tam giác SCD nên EF{\rm{//}}CD. Suy ra IJ{\rm{//}}EF, nên A đúng.
Do đó chọn đáp án C.
Câu 5: Chọn D.
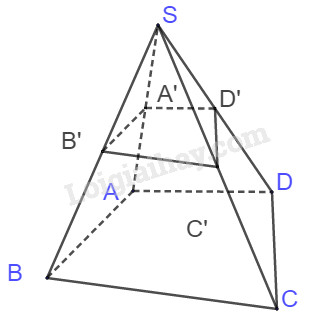
A'B' là đường trung bình của tam giác SAB nên A'B'//AB.
Câu 6: Chọn C
Câu 7: Chọn B
Câu 8: Chọn D
Câu 9: Chọn C

