Video hướng dẫn giải
Giải các phương trình sau:
LG a
sin3x−cos5x=0
Phương pháp giải:
B1: chuyển vế, đưa PT về dạng sinα=cosβ.
B2: Do sinx=cos(π2−x) PT trở về dạng cosX=cosY với X=(π2−x);Y=β
⇔[X=Y+k2πX=−Y+k2π(k∈Z)
Từ đó suy ra nghiệm x và KL.
Lời giải chi tiết:
sin3x−cos5x=0⇔cos5x=sin3x=cos(π2−3x)⇔[5x=π2−3x+k2π5x=−π2+3x+k2π⇔[8x=π2+k2π2x=−π2+k2π⇔[x=π16+kπ4x=−π4+kπ(k∈Z)
Vậy nghiệm phương trình là: x=π16+kπ4(k∈Z) và x=−π4+kπ,(k∈Z)
Cách khác:
sin3x - cos5x = 0
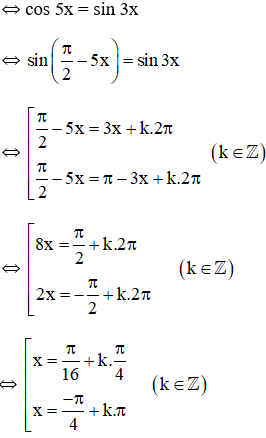
Vậy nghiệm phương trình là: x=π16+kπ4(k∈Z) và x=−π4+kπ,(k∈Z)
LG b
tan3xtanx=1
Phương pháp giải:
B1: Tìm ĐKXĐ.
B2: vì 1tanx=cotx=tan(π2−x)
phương trình trở về dạng tanα=tanβ với α=3x;β=π2−x
⇔α=β+kπ(k∈Z)
B3: Suy ra nghiệm x rồi KL.
Lời giải chi tiết:
Điều kiện:
{cos3x≠0cosx≠0⇔{3x≠π2+kπx≠π2+kπ⇔{x≠π6+kπ3x≠π2+kπ⇒x≠π6+kπ3(k∈Z)
tan3xtanx=1⇔tan3x=1tanx⇔tan3x=cotx⇔tan3x=tan(π2−x)⇔3x=π2−x+kπ⇔4x=π2+kπ⇔x=π8+kπ4(k∈Z)(tm)
Vậy nghiệm phương trình là x=π8+kπ4,k∈Z.
Chú ý:
Ở bài này ta thấy ngay họ nghiệm x=π8+kπ4,k∈Z không có nghiệm nào vi phạm điều kiện xác định nên ta lấy cả họ nghiệm và không phải loại bỏ điểm nào.

