Đề bài
Cho hai mặt phẳng (α)(α) và (β)(β) vuông góc với nhau. Người ta lấy trên giao tuyến ΔΔ của hai mặt phẳng đó hai điểm AA và BB sao cho AB=8cmAB=8cm. Gọi CC là một điểm trên (α)(α) và DD là một điểm trên (β)(β) sao cho ACAC và BDBD cùng vuông góc với giao tuyến ΔΔ và AC=6cmAC=6cm, BD=24cmBD=24cm. Tính độ dài đoạn CDCD.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Chứng minh AC⊥ADAC⊥AD và sử dụng định lý Pi-ta-go để tính toán.
Lời giải chi tiết
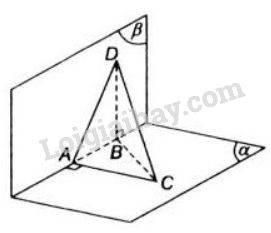
(α)⊥(β)AC⊥ΔAC⊂(α)}⇒AC⊥(β)
Do đó AC⊥AD hay tam giác ACD vuông tại A
Áp dụng định lí Pytago vào tam giác ACD ta được: DC2=AC2+AD2(1)
Vì BD⊥AB⇒ΔABD vuông tại B.
Áp dụng định lí Pytago vào tam giác ABD ta được: AD2=AB2+BD2(2)
Từ (1) và (2) suy ra: DC2=AC2+AB2+BD2=62+82+242=676
⇒DC=√676=26cm

