Đề bài
I. TRẮC NGHIỆM (6 ĐIỂM)
Câu 1: Hàm số nào sau đây là hàm số chẵn?
A. f(x)=1+tanx B. f(x)=x2+cos(3x)
C. f(x)=x2sin(2x) D. f(x)=−cotx
Câu 2: Hàm số nào sau đây có tập xác định là R?
A. y=sin√x B. y=12−cosx
C. y=tan2x D. y=1−sinx1+sinx
Câu 3: Tìm a để phương trình (a−1)cosx=1 có nghiệm.
A. 0≤a≤2,a≠1 B. [a≤0a≥2
C. a≥2 D. a≤0
Câu 4: Cho hình chóp S.ABCD, I là trung điểm của SC, giao điểm của AI và (SBD) là :
A. Điểm K (với O là trung điểm của BD và K=SO∩AI)
B. Điểm M (với O=AC∩BD;M=SO∩AI)
C. Điểm N (với O=AC∩BD; N là trung điểm SO)
D. Điểm I.
Câu 5: Nghiệm của phương trình sin(x+π6)=12 là:
A. [x=π3+k2πx=2π3+k2π(k∈Z)
B. [x=k2πx=2π3+k2π(k∈Z)
C. [x=kπx=2π3+kπ(k∈Z)
D. [x=π6+k2πx=5π6+k2π(k∈Z)
Câu 6: Nghiệm dương nhỏ nhất của phương trình tanx=−1 là:
A. π4 B. 7π4
C. 3π4 D. −π4
Câu 7: Khẳng định nào sau đây sai?
A. y=cotx nghịch biến trên khoảng (π2;π).
B. y=sinx nghịch biến trên khoảng (π2;π).
C. y=−cosx đồng biến trên khoảng (π3;π2).
D. y=−tanx đồng biến trên khoảng (π3;π2).
Câu 8: Nghiệm của phương trình sin2x−√3sinx=0 là:
A. [x=kπx=π6+k2π(k∈Z)
B. [x=kπx=±π3+k2π(k∈Z)
C. [x=kπx=±π6+k2π(k∈Z)
D. [x=k2πx=±π6+k2π(k∈Z)
Câu 9: Gọi a là nghiệm của phương trình 2cos2x+cosx−1=0 trên khoảng (0;π2). Tính cos2a.
A. −12 B. π3 C. 12 D. −π3
Câu 10: Trong hệ trục tọa độ Oxy, cho →v(3;3) và đường tròn (C):(x−1)2+(y+2)2=9. Tìm phương trình đường tròn (C′) là ảnh của (C) qua phép tịnh tiến T→v.
A. (C′):(x−4)2+(y−1)2=9
B. (C′):(x−2)2+(y−5)2=9
C. (C′):(x+4)2+(y+1)2=9
D. (C′):(x−4)2+(y−1)2=3.
Câu 11: Nghiệm của phương trình sinx.cosx.(sin2x−cos2x)=0 là:
A. x=kπ2(k∈Z) B. x=kπ(k∈Z)
C. x=kπ8(k∈Z) D. x=kπ4(k∈Z)
Câu 12: Cho các mệnh đề sai:
(1) Hàm số y=sinx và y=cosx cùng đồng biến trên khoảng (3π2;2π).
(2) Đồ thị hàm số y=2019sinx+10cosx cắt trục hoành tại vô số điểm.
(3) Đồ thị hàm số y=tanx và y=cotx trên khoảng (0;π) chỉ có một điểm chung.
(4) Với ∈(π;3π2) các hàm số y=tan(π−x), y=cot(π−x), y=sin(π−x) đều nhận giá trị âm.
Trong các mệnh đề trên, số mệnh đề sai là:
A. 0 B. 2 C. 3 D. 1
Câu 13: Hàm số nào sau đây toàn hoàn với chu kì 2π?
A. y=tan(x2) B. y=sin2x
C. y=cos(x2) D. y=cot2x
Câu 14: Cho hình chóp S.ABCD có đáy ABCD là tứ giác lồi. Gọi Olà giao điểm của AC và BD, Mlà giao điểm của AB và CD, Nlà giao điểm của AD và BC. Giao tuyến của hai mặt phẳng (SAB)và (SCD)là?
A. SA B. SN C. SM D. SO
Câu 15: Tìm số giá trị nguyên của m thuộc đoạn [−2019;2019] để phương trình sau có nghiệm
2sin2x+(m−1)cos2x=m+1
A. 2021 B. 2020 C. 4038 D. 4040
II. TỰ LUẬN (4 ĐIỂM)
Câu 1 (0.5 điểm): Tìm tập xác định của hàm số y=cot(2x)cos(2x).
Câu 2 (0.5 điểm): Giải phương trình cos2x−3sinx+3=0.
Câu 3 (1 điểm): Tìm a để phương trình (2sinx−1)(cosx−a)=0 có đúng hai nghiệm thuộc (0;π).
Câu 4 (1 điểm): Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số f(x)=x+cos2x trên đoạn [0;π4].
Câu 5 (1 điểm): Cho hình chóp S.ABC với M, N lần lượt là trung điểm của SB, AB; P thuộc đoạn AC sao cho AP = 2PC.
1. Xác định giao tuyến của các cặp mặt phẳng sau:
1.1. (MNP) và (ABC). 1.2. (MNP) và (SBC).
2. Xác định giao điểm Q của mặt phẳng (MNP) với SC. Tính PQ khi biết SA =12cm.
Lời giải chi tiết
I. TRẮC NGHIỆM (6 ĐIỂM)
| 1. B | 2. B | 3. B | 4. B | 5. B |
| 6. C | 7. C | 8. C | 9. A | 10. A |
| 11. D | 12. D | 13. A | 14. C | 15. A |
Câu 1:
Phương pháp:
Cho hàm số y=f(x) có tập xác định D.
- Hàm số y=f(x) là hàm số chẵn nếu {∀x∈D⇒−x∈Df(−x)=f(x).
- Hàm số y=f(x) là hàm số lẻ nếu {∀x∈D⇒−x∈Df(−x)=−f(x).
Cách giải:
Xét đáp án A:
TXĐ: D=R∖{π2+kπ} ⇒∀x∈D⇒−x∈D.
Ta có: f(−x)=1+tan(−x)=1−tanx≠f(x)
⇒ Hàm số f(x)=1+tanx là hàm không chẵn, không lẻ.
Xét đáp án B:
TXĐ: D=R.
Ta có: f(−x)=(−x)2+cos(−3x)=x2+cos(3x)=f(x).
⇒ Hàm số f(x)=x2+cos(3x) là hàm chẵn.
Chọn B.
Câu 2:
Phương pháp:
Sử dụng tính chất: −1≤cosx≤1 ∀x∈R.
Cách giải:
Xét đáp án B:
Vì −1≤cosx≤1∀x∈R ⇔1≤2−cosx≤3∀x∈R.
Do đó 2−cosx≠0∀x∈R.
Vậy hàm số y=12−cosx có TXĐ là R.
Chọn B.
Câu 3:
Phương pháp:
- Biện luận phương trình bậc nhất ax+b=0.
- Sử dụng tính chất: −1≤cosx≤1 ∀x∈R.
Cách giải:
TH1: a−1=0⇔a=1, khi đó phương trình trở thành 0.cosx=1 (Vô nghiệm).
TH2: a−1≠0⇔a≠1, khi đó ta có cosx=1a−1(a≠1).
Vì −1≤cosx≤1∀x∈R ⇒−1≤1a−1≤1∀x∈R.
⇔{1a−1≥−11a−1≤1⇔{1+a−1a−1≥01−a+1a−1≤0⇔{aa−1≥02−aa−1≤0⇔{[a>1a≤0[a≥2a<1⇔[a≥2a≤0(tma≠1)
Vậy [a≥2a≤0.
Chọn B.
Câu 4:
Phương pháp:
Tìm giao điểm của đường và mặt.
Cách giải:
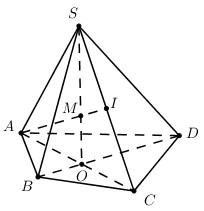
Trong (ABCD) gọi O=AC∩BD.
Trong (SAC) gọi M=SO∩AI ta có
M∈SO⊂(SBD)⇒M∈(SBD)⇒M=AI∩(SBD) với O=AC∩BD;M=SO∩AI.
Chọn B.
Câu 5:
Phương pháp:
Giải phương trình lượng giác cơ bản: sinx=sinα⇔[x=α+k2πx=π−α+k2π(k∈Z).
Cách giải:
Ta có:
sin(x+π6)=12⇔sin(x+π6)=sinπ6⇔[x+π6=π6+k2πx+π6=5π6+k2π⇔[x=k2πx=2π3+k2π(k∈Z)
Chọn B.
Câu 6:
Phương pháp:
- Giải phương trình lượng giác cơ bản: \tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi \,\,\left( {k \in \mathbb{Z}} \right).
- Giải bất phương trình x > 0, tìm số nguyên k nhỏ nhất thỏa mãn.
Cách giải:
Ta có: \tan x = - 1 \Leftrightarrow x = - \dfrac{\pi }{4} + k\pi \,\,\left( {k \in \mathbb{Z}} \right).
Xét x > 0 \Leftrightarrow - \dfrac{\pi }{4} + k\pi > 0 \Leftrightarrow k > \dfrac{1}{4}.
\Rightarrow Số nguyên k nhỏ nhất thỏa mãn điều kiện là {k_{\min }} = 1.
Vậy nghiệm dương nhỏ nhất của phương trình đã cho là x = - \dfrac{\pi }{4} + \pi = \dfrac{{3\pi }}{4}.
Chọn C.
Câu 7:
Phương pháp:
Dựa vào đồ thị các hàm số lượng giác.
Cách giải:
Đồ thị hàm số y = \cot x:
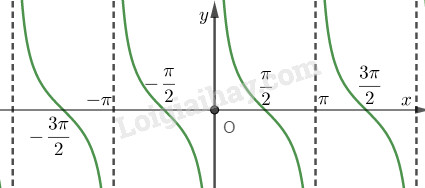
\Rightarrow Hàm số nghịch biến trên khoảng \left( {\dfrac{\pi }{2};\pi } \right) là khẳng định đúng.
Đồ thị hàm số y = \sin x:
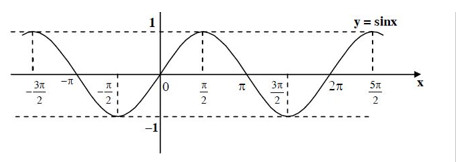
\Rightarrow Hàm số y = \sin x nghịch biến trên khoảng \left( {\dfrac{\pi }{2};\pi } \right) là mệnh đề ĐÚNG.
Đồ thị hàm số y = \cos x:
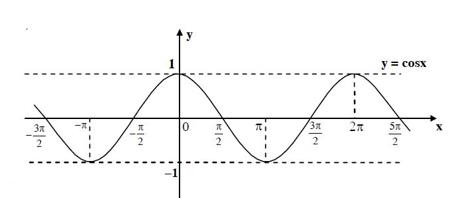
\Rightarrow Hàm số y = \cos x đồng biến trên khoảng \left( {\dfrac{\pi }{3};\dfrac{\pi }{2}} \right) \Rightarrow Hàm số y = - \cos x nghịch biến trên khoảng \left( {\dfrac{\pi }{3};\dfrac{\pi }{2}} \right). Do đó mệnh đề C sai.
Chọn C.
Câu 8:
Phương pháp:
- Sử dụng công thức nhân đôi \sin 2x = 2\sin x\cos x .
- Đưa phương trình về dạng tích sau đó giải phương trình lượng giác cơ bản.
Cách giải:
Ta có:
\begin{array}{l}\,\,\,\,\,\sin 2x - \sqrt 3 \sin x = 0\\ \Leftrightarrow 2\sin x\cos x - \sqrt 3 \sin x = 0\\ \Leftrightarrow \sin x\left( {2\cos x - \sqrt 3 } \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}\sin x = 0\\\cos x = \dfrac{{\sqrt 3 }}{2}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = k\pi \\x = \pm \dfrac{\pi }{6} + k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\end{array}
Chọn C.
Câu 9:
Phương pháp:
- Giải phương trình bậc hai đối với một hàm số lượng giác tìm \cos x.
- Chú ý điều kiện x \in \left( {0;\dfrac{\pi }{2}} \right) \Rightarrow \cos x > 0.
- Sử dụng công thức nhân đôi: \cos 2a = 2{\cos ^2}a - 1.
Cách giải:
Ta có: 2{\cos ^2}x + \cos x - 1 = 0 \Leftrightarrow \left[ \begin{array}{l}\cos x = \dfrac{1}{2}\\\cos x = - 1\end{array} \right..
Vì x \in \left( {0;\dfrac{\pi }{2}} \right) \Rightarrow \cos x > 0, do đó \cos x = \dfrac{1}{2}.
Vậy \cos 2a = 2{\cos ^2}a - 1 = 2.{\left( {\dfrac{1}{2}} \right)^2} - 1 = - \dfrac{1}{2}.
Chọn A.
Câu 10:
Phương pháp:
Áp dụng tính chất của phép tịnh tiến điểm M thành M’ theo vecto v thì \overrightarrow {MM'} {\rm{\;}} = \vec v.
Cách giải:
Đường tròn (C): {\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 9có tâm I(1;-2); bán kinh R=3.
Gọi I’ là tâm đường tròn (C’).
Phép tịnh tiến điểm I thành điểm I’ theo véc-tơ \vec v\left( {3;3} \right)thì \overrightarrow {II'} {\rm{\;}} = \vec v
Suy ra I'\left( {4;1} \right)
Đường tròn (C’) có tâm là I'\left( {4;1} \right); R=3 nên có dạng {\left( {x - 4} \right)^2} + {\left( {y - 1} \right)^2} = 9
Chọn A.
Câu 11:
Phương pháp:
- Sử dụng công thức nhân đôi: \sin 2\alpha = 2\sin \alpha \cos \alpha ,\,\,cos2\alpha = co{s^2}\alpha - {\sin ^2}\alpha .
- Giải phương trình lượng giác cơ bản: \sin x = 0 \Leftrightarrow x = k\pi .
Cách giải:
Ta có:
\begin{array}{l}\,\,\,\,\,\,\sin x.\cos x.\left( {{{\sin }^2}x - {{\cos }^2}x} \right) = 0\\ \Leftrightarrow - \dfrac{1}{2}\sin 2x.\cos 2x = 0 \Leftrightarrow - \dfrac{1}{4}\sin 4x = 0\\ \Leftrightarrow \sin 4x = 0 \Leftrightarrow x = \dfrac{{k\pi }}{4}\,\,\left( {k \in \mathbb{Z}} \right)\end{array}
Chọn D.
Câu 12:
Phương pháp:
- Mệnh đề (1): Sử dụng đồ thị hàm số.
- Mệnh đề (2), (3): Xét phương trình hoành độ giao điểm.
- Mệnh đề 4: Sử dụng tính chất “sin bù”.
Cách giải:
Xét mệnh đề (1): Ta có đồ thị hàm số y = \sin x và y = \cos x như sau:
Đồ thị hàm số y = \sin x:
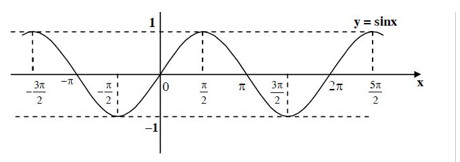
Đồ thị hàm số y = \cos x:
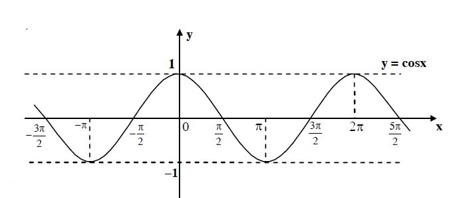
Hai hàm số này cùng đồng biến trên \left( {\dfrac{{3\pi }}{2};2\pi } \right). Do đó mệnh đề (1) đúng.
Xét mệnh đề (2): Phương trình hoành độ giao điểm: 2019\sin x + 10\cos x = 0 \Leftrightarrow \tan x = - \dfrac{{10}}{{2019}}.
Do đó phương trình này có vô số nghiệm, nên mệnh đề (2) đúng.
Xét mệnh đề (3): Phương trình hoành độ giao điểm:
\tan x = \cot x \Leftrightarrow \tan x = \dfrac{1}{{\tan x}} \Leftrightarrow \left[ \begin{array}{l}\tan x = 1\\\tan x = - 1\end{array} \right. \Rightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{4} + k\pi \\x = - \dfrac{\pi }{4} + k\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right) .
+ Xét họ nghiệm x = \dfrac{\pi }{4} + k\pi .
0 < \dfrac{\pi }{4} + k\pi < \pi \Leftrightarrow - \dfrac{1}{4} < k < \dfrac{3}{4},\,\,k \in \mathbb{Z} \Rightarrow k = 0 \Rightarrow x = \dfrac{\pi }{4}.
+ Xét họ nghiệm x = - \dfrac{\pi }{4} + k\pi .
0 < - \dfrac{\pi }{4} + k\pi < \pi \Leftrightarrow \dfrac{1}{4} < k < \dfrac{5}{4},\,\,k \in \mathbb{Z} \Rightarrow k = 1 \Rightarrow x = \dfrac{{3\pi }}{4}.
Vậy đồ thị hàm số y = \tan x và y = \cot x trên khoảng \left( {0;\pi } \right) có 2 điểm chung, do đó mệnh đề (3) sai.
Xét mệnh đề (4):
Ta có: \tan \left( {\pi - x} \right) = - \tan x,\,\,\cot \left( {\pi - x} \right) = - \cot x,\,\,\sin \left( {\pi - x} \right) = \sin x.
Trên khoảng \left( {\pi ;\dfrac{{3\pi }}{2}} \right) ta có: \left\{ \begin{array}{l}\tan x > 0 \Leftrightarrow - \tan x < 0\\\cot x > 0 \Leftrightarrow - \cot x < 0\\\sin x < 0\end{array} \right..
Do đó mệnh đề (4) đúng.
Vậy có 1 mệnh đề sai.
Chọn D.
Câu 13:
Phương pháp:
- Hàm số y = \sin ax,\,\,y = \cos ax tuần hoàn với chu kì T = \dfrac{{2\pi }}{{\left| a \right|}}.
- Hàm số y = \tan ax,\,\,y = \cot ax tuần hoàn với chu kì T = \dfrac{\pi }{{\left| a \right|}}.
Cách giải:
Hàm số y = \tan \left( {\dfrac{x}{2}} \right) tuần hoàn với chu kì T = \dfrac{\pi }{{\dfrac{1}{2}}} = 2\pi .
Chọn A.
Câu 14:
Phương pháp:
Xác định hai điểm chung của hai mặt phẳng.
Cách giải:
Xét \left( {SAB} \right) và \left( {SCD} \right) có:
+ S là điểm chung thứ nhất.
+ M = AB \cap CD \Rightarrow \left\{ {\begin{array}{*{20}{l}}{M \in AB \subset \left( {SAB} \right) \Rightarrow M \in \left( {SAB} \right)}\\{M \in CD \subset \left( {SCD} \right) \Rightarrow M \in \left( {SCD} \right)}\end{array}} \right.
\Rightarrow M \in \left( {SAB} \right) \cap \left( {SCD} \right) \Rightarrow M là điểm chung thứ hai.
Vậy \left( {SAB} \right) \cap \left( {SCD} \right) = SM.
Chọn C.
Câu 15:
Phương pháp:
Phương trình dạng a\sin x + b\cos x = c có nghiệm khi và chỉ khi {a^2} + {b^2} \ge {c^2}.
Cách giải:
Phương trình 2\sin 2x + \left( {m - 1} \right)\cos 2x = m + 1 có nghiệm khi và chỉ khi:
\begin{array}{l}\,\,\,\,\,{2^2} + {\left( {m - 1} \right)^2} \ge {\left( {m + 1} \right)^2}\\ \Leftrightarrow 4 + {m^2} - 2m + 1 \ge {m^2} + 2m + 1\\ \Leftrightarrow 4m \le 4 \Leftrightarrow m \le 1\end{array}
Kết hợp điều kiện m \in \left[ { - 2019;2019} \right] \Rightarrow m \in \left[ { - 2019;1} \right].
Vậy có 2021 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Chọn A.
II. TỰ LUẬN (4 ĐIỂM)
Câu 1:
Phương pháp:
- Hàm phân thức xác định khi và chỉ khi mẫu thức khác 0.
- Hàm \cot x xác định khi và chỉ khi \sin x \ne 0.
Cách giải:
Hàm số y = \dfrac{{\cot \left( {2x} \right)}}{{\cos \left( {2x} \right)}} xác định \Leftrightarrow \left\{ \begin{array}{l}\sin 2x \ne 0\\\cos 2x \ne 0\end{array} \right. \Leftrightarrow \sin 4x \ne 0 \Leftrightarrow 4x \ne k\pi \Leftrightarrow x \ne \dfrac{{k\pi }}{4}.
Vậy TXĐ của hàm số là D = \mathbb{R}\backslash \left\{ {\dfrac{{k\pi }}{4};\,\,k \in \mathbb{Z}} \right\}.
Câu 2:
Phương pháp:
- Sử dụng công thức {\cos ^2}x = 1 - {\sin ^2}x, đưa phương trình về dạng phương trình bậc hai đối với một hàm số lượng giác.
- Giải phương trình bậc hai, sau đó giải phương trình lượng giác cơ bản.
Cách giải:
Ta có:
\begin{array}{l}\,\,\,\,\,\,{\cos ^2}x - 3\sin x + 3 = 0\\ \Leftrightarrow 1 - {\sin ^2}x - 3\sin x + 3 = 0\\ \Leftrightarrow {\sin ^2}x + 3\sin x - 4 = 0\\ \Leftrightarrow \left[ \begin{array}{l}\sin x = 1\\\sin x = - 4\,\,\left( {KTM} \right)\end{array} \right.\\ \Leftrightarrow x = \dfrac{\pi }{2} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\end{array}
Vậy nghiệm của phương trình là x = \dfrac{\pi }{2} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right).
Câu 3:
Phương pháp:
- Giải phương trình tích.
- Giải phương trình lượng giác cơ bản, tìm số nghiệm của phương trình trong khoảng \left( {0;\pi } \right), sau đó biện luận số nghiệm của phương trình chứa tham số.
Cách giải:
Ta có:
\begin{array}{l}\,\,\,\,\,\,\left( {2\sin x - 1} \right)\left( {\cos x - a} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2\sin x - 1 = 0\\\cos x - a = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\sin x = \dfrac{1}{2}\\\cos x = a\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{6} + k2\pi \\x = \dfrac{{5\pi }}{6} + k2\pi \\\cos x = a\,\,\left( * \right)\end{array} \right.\end{array}
Họ nghiệm x = \dfrac{\pi }{6} + k2\pi có 1 nghiệm x = \dfrac{\pi }{6} \in \left( {0;\pi } \right).
Họ nghiệm x = \dfrac{{5\pi }}{6} + k2\pi có 1 nghiệm x = \dfrac{{5\pi }}{6} \in \left( {0;\pi } \right).
Do đó để phương trình ban đầu có đúng 2 nghiệm thuộc \left( {0;\pi } \right) thì hoặc phương trình (*) vô nghiệm, hoặc phương trình (*) có nghiệm x = \dfrac{\pi }{6} hoặc x = \dfrac{{5\pi }}{6}.
TH1: (*) vô nghiệm \Rightarrow \left[ \begin{array}{l}a > 1\\a < - 1\end{array} \right..
TH2: (*) có nghiệm x = \dfrac{\pi }{6}.
\Rightarrow \cos \dfrac{\pi }{6} - a = 0 \Leftrightarrow a = \dfrac{{\sqrt 3 }}{2}.
Thử lại: Với a = \dfrac{{\sqrt 3 }}{2} \Rightarrow \cos x = \dfrac{{\sqrt 3 }}{2} \Leftrightarrow x = \pm \dfrac{\pi }{6} + k2\pi có đúng 1 nghiệm x = \dfrac{\pi }{6} \in \left( {0;\pi } \right).
TH3: (*) có nghiệm x = \dfrac{{5\pi }}{6}.
\Rightarrow \cos \dfrac{{5\pi }}{6} - a = 0 \Leftrightarrow a = - \dfrac{{\sqrt 3 }}{2}.
Thử lại: Với a = - \dfrac{{\sqrt 3 }}{2} \Rightarrow \cos x = - \dfrac{{\sqrt 3 }}{2} \Leftrightarrow x = \pm \dfrac{{5\pi }}{6} + k2\pi có đúng 1 nghiệm x = \dfrac{{5\pi }}{6} \in \left( {0;\pi } \right).
Vậy a \in \left( { - \infty ; - 1} \right) \cup \left( {1; + \infty } \right) \cup \left\{ { \pm \dfrac{{\sqrt 3 }}{2}} \right\}.
Câu 4:
Cách giải:
Giả sử {x_1},\,\,{x_2} \in \left[ {0;\dfrac{\pi }{4}} \right];\,\,{x_1} < {x_2}.
Xét
\begin{array}{l}f\left( {{x_2}} \right) - f\left( {{x_1}} \right) = \left( {{x_2} - {x_1}} \right) + {\cos ^2}\left( {{x_2}} \right) - {\cos ^2}\left( {{x_1}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {{x_2} - {x_1}} \right) + \left( {\cos {x_2} + \cos {x_1}} \right)\left( {\cos {x_2} - \cos {x_1}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {{x_2} - {x_1}} \right) - 4\cos \dfrac{{{x_2} + {x_1}}}{2}\cos \dfrac{{{x_2} - {x_1}}}{2}.sin\dfrac{{{x_2} + {x_1}}}{2}.\sin \dfrac{{{x_2} - {x_1}}}{2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {{x_2} - {x_1}} \right) - \left( {2sin\dfrac{{{x_2} + {x_1}}}{2}\cos \dfrac{{{x_2} + {x_1}}}{2}} \right)\left( {2\sin \dfrac{{{x_2} - {x_1}}}{2}\cos \dfrac{{{x_2} - {x_1}}}{2}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {{x_2} - {x_1}} \right) - \sin \left( {{x_2} + {x_1}} \right)\sin \left( {{x_2} - {x_1}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \ge \left( {{x_2} - {x_1}} \right) - \sin \left( {{x_2} - {x_1}} \right)\end{array}
Vì 0 < {x_2} - {x_1} \le \dfrac{\pi }{4} \Rightarrow x > \sin x, do đó \left( {{x_2} - {x_1}} \right) - \sin \left( {{x_2} - {x_1}} \right) > 0\,\,\forall x \in \left[ {0;\dfrac{\pi }{4}} \right].
Suy ra hàm số f\left( x \right) = x + {\cos ^2}x đồng biến trên đoạn \left[ {0;\dfrac{\pi }{4}} \right].
\Rightarrow f\left( 0 \right) = 1 \le f\left( x \right) \le f\left( {\dfrac{\pi }{4}} \right) = \dfrac{\pi }{4} + \dfrac{1}{2}\,\,\forall x \in \left[ {0;\dfrac{\pi }{4}} \right].
Vậy GTLN của hàm số bằng \dfrac{\pi }{4} + \dfrac{1}{2}, đạt được tại x = \dfrac{\pi }{4} và GTNN của hàm số bằng 1, đạt được tại x = 0.
Câu 5:
Phương pháp:
1. Xác định giao tuyến của các mặt phẳng bằng cách xác định các điểm chung.
2. Chứng minh PQ // SA bằng cách áp dụng định lí Ta-lét đảo, từ đó áp dụng định lí Ta-lét tính PQ.
Cách giải:
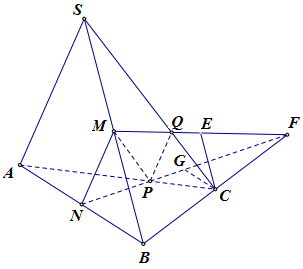
1.
1.1. Xác định giao điểm của (MNP) và (ABC)
Ta có: N, P là hai điểm chung của hai mạt phẳng (MNP) và (ABC) \Rightarrow \left( {MNP} \right) \cap \left( {ABC} \right) = NP.
1.2. Xác định giao điểm của (MNP) và (SBC).
Trong (ABC) gọi F = NP \cap BC
Vì F \in BC \subset \left( {SBC} \right) \Rightarrow F \in \left( {SBC} \right). Trong (SBC) gọi Q = MF \cap SC.
\Rightarrow \left( {MNP} \right) \cap \left( {SBC} \right) = MQ.
2. Theo 1.2 ta đã xác định được Q = MF \cap SC. Mà MF \subset \left( {MNP} \right) \Rightarrow Q = SC \cap \left( {MNP} \right).
Trong (ABC), lấy G \in NF sao cho GC//AB.
Áp dụng định lí Ta-lét ta có: \dfrac{{GC}}{{AN}} = \dfrac{{PC}}{{AP}} = \dfrac{1}{2} \Rightarrow GC = \dfrac{1}{2}AN. Mà AN = BN{\mkern 1mu} {\mkern 1mu} \left( {gt} \right) \Rightarrow GC = \dfrac{1}{2}BN.
\Rightarrow \dfrac{{GC}}{{BN}} = \dfrac{{FG}}{{FN}} = \dfrac{{FC}}{{FB}} = \dfrac{1}{2} \Rightarrow C là trung điểm của BF.
Trong (SBC) kẻ EC//SB{\mkern 1mu} {\mkern 1mu} \left( {E \in MF} \right) .
Xét tam giác FBM có :
C là trung điểm của BF (cmt);
EC//SB
\Rightarrow E là trung điểm của MF (Định lí đường trung bình của tam giác).
\Rightarrow EC là đường trung bình của tam giác FMB \Rightarrow \dfrac{{EC}}{{MB}} = \dfrac{1}{2}. Mà MB = SM \Rightarrow \dfrac{{EC}}{{SM}} = \dfrac{1}{2}
Áp dụng định lí Ta-lét ta có: \dfrac{{EC}}{{SM}} = \dfrac{{QC}}{{SQ}} = \dfrac{1}{2}. Mà AP = 2PC{\mkern 1mu} {\mkern 1mu} \left( {gt} \right) \Rightarrow \dfrac{{PC}}{{AP}} = \dfrac{1}{2} \Rightarrow \dfrac{{QC}}{{SQ}} = \dfrac{{PC}}{{AP}} \Rightarrow PQ//SA (định lí Ta-lét đảo) và \dfrac{{PQ}}{{SA}} = \dfrac{{PC}}{{AC}} = \dfrac{1}{3} \Rightarrow PQ = \dfrac{1}{3}SA = \dfrac{1}{3}.12 = 4{\mkern 1mu} {\mkern 1mu} \left( {cm} \right).

