Video hướng dẫn giải
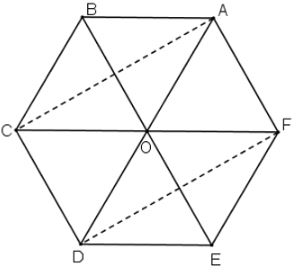
Cho lục giác đều \(ABCDEF\) tâm \(O\). Tìm ảnh của tam giác \(AOF\).
LG a
Qua phép tịnh tiến theo vectơ \(AB\)
Phương pháp giải:
Để tìm ảnh của một tam giác qua phép tịnh tiến, ta tìm ảnh của từng đỉnh qua phép tịnh tiến. Tam giác tạo bởi 3 đỉnh mới chính là ảnh cần tìm.
Lời giải chi tiết:
Ta có: \(\overrightarrow {AB} = \overrightarrow {AB} \Rightarrow {T_{\overrightarrow {AB} }}\left( A \right) = B\),
\(\overrightarrow {OC} = \overrightarrow {AB} \Rightarrow {T_{\overrightarrow {AB} }}\left( O \right) = C\),
\(\overrightarrow {FO} = \overrightarrow {AB} \Rightarrow {T_{\overrightarrow {AB} }}\left( F \right) = O\).
Do đó \({T_{\overrightarrow {AB} }}\left( {\Delta AOF} \right) = \Delta BCO\).
LG b
Qua phép đối xứng qua đường thẳng \(BE\)
Phương pháp giải:
Để tìm ảnh của một tam giác qua phép đối xứng, ta tìm ảnh của từng đỉnh qua phép đối xứng ấy. Tam giác tạo bởi 3 đỉnh mới chính là ảnh cần tìm.
Lời giải chi tiết:
Theo tính chất hình lục giác đều thì:
+) \(A,C\) đối xứng nhau qua \(BE\).
+) \(O\) đối xứng với chính nó qua \(BE\).
+) \(F,D\) đối xứng nhau qua \(BE\).
Từ đó ta có:
\(\left\{ \begin{array}{l}{D_{BE}}\left( A \right) = C\\{D_{BE}}\left( O \right) = O\\{D_{BE}}\left( F \right) = D\end{array} \right. \) \(\Rightarrow {D_{BE}}\left( {\Delta AOF} \right) = COD\)
LG c
Qua phép quay tâm \(O\) góc \( 120^{\circ}\)
Phương pháp giải:
Để tìm ảnh của một tam giác qua phép quay, ta tìm ảnh của từng đỉnh qua phép quay đó. Tam giác tạo bởi 3 đỉnh mới chính là ảnh cần tìm.
Lời giải chi tiết:
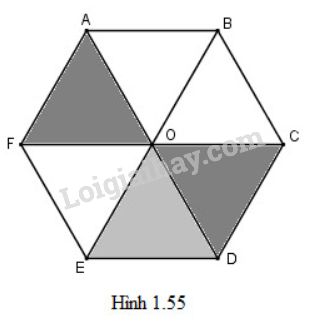
Ta có: \(\left( {\overrightarrow {OA} ,\overrightarrow {OE} } \right) = \widehat {AOE} = {120^0}\), \(\left( {\overrightarrow {OF} ,\overrightarrow {OD} } \right) = \widehat {FOD} = {120^0}\).
Do đó \(\left\{ \begin{array}{l}{Q_{\left( {O;{{120}^0}} \right)}}\left( A \right) = E\\{Q_{\left( {O;{{120}^0}} \right)}}\left( O \right) = O\\{Q_{\left( {O;{{120}^0}} \right)}}\left( F \right) = D\end{array} \right. \\\Rightarrow {Q_{\left( {O;{{120}^0}} \right)}}\left( {\Delta AOF} \right) = \Delta EOD\)
Chú ý:
Trong câu này do không nói các đỉnh đặt theo chiều nào của kim đồng hồ nên sẽ có hai kết quả. Trên đã trình bày theo trường hợp A, B, C, D, E, F đặt cùng chiều quay kim đồng hồ. Các em tham khảo thêm trường hợp A, B, C, D, E, F đặt ngược chiều quay kim đồng hồ như sau:
Ta có:\(OA = OB = OC = OF\)
\((OA;OC) = {120^o};\;\;\;(OF;OB) = {120^o}\)
\(\begin{array}{l}
\Rightarrow \left\{ {\begin{array}{*{20}{l}}
{{Q_{\left( {O;{{120}^0}} \right)}}\left( A \right) = C}\\
{{Q_{\left( {O;{{120}^0}} \right)}}\left( O \right) = O}\\
{{Q_{\left( {O;{{120}^0}} \right)}}\left( F \right) = B}
\end{array}} \right.\quad \\
\Rightarrow {Q_{\left( {O;{{120}^0}} \right)}}\left( {\Delta AOF} \right) = \Delta COB.
\end{array}\)