Video hướng dẫn giải
Gieo đồng thời hai con súc sắc. Tính xác suất sao cho:
LG a
Hai con xúc sắc đều xuất hiện mặt chẵn
Phương pháp giải:
Tính số phần tử của không gian mẫu \(n\left( \Omega \right)\)
Tính số phần tử của biến cố A: \(n\left( A \right)\).
Tính xác suất của biến cố A: \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega \right)}}\).
Lời giải chi tiết:
Không gian mẫu là: \(\Omega = \left\{ {(i,j) |1\le i,j \le 6} \right\}\) \( \Rightarrow n(\Omega ) = {6^2} = 36\)
\(A\) là biến cố “Hai con xúc sắc đều xuất hiện mặt chẵn”
Suy ra:
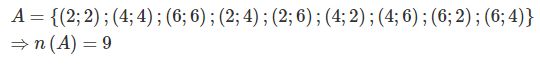
Vậy \(\displaystyle P(A) = {9 \over {36}} = {1 \over 4}\)
LG b
Tích các số chấm trên hai con xúc sắc là số lẻ.
Phương pháp giải:
Tính số phần tử của không gian mẫu \(n\left( \Omega \right)\)
Tính số phần tử của biến cố A: \(n\left( A \right)\).
Tính xác suất của biến cố A: \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega \right)}}\).
Lời giải chi tiết:
Gọi \(B\) là biến cố: “Tích các số chấm trên hai con xúc sắc là số lẻ”.
Tích của hai số là số lẻ khi và chỉ khi cả hai số đều là số lẻ. Khi đó ta có:
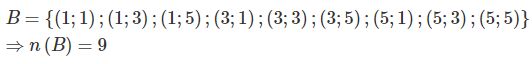
Vậy \(\displaystyle P(B) = {9 \over {36}} = {1 \over 4}\)
Chú ý: Do bài cho là hai con xúc sắc nên không gian mẫu luôn có \(36\) phần tử, hai con xúc sắc khác nhau nên các trường hợp đảo vị trí của hai kết quả đều được tính (chỉ đối với hai kết quả ra mặt khác nhau).

