Video hướng dẫn giải
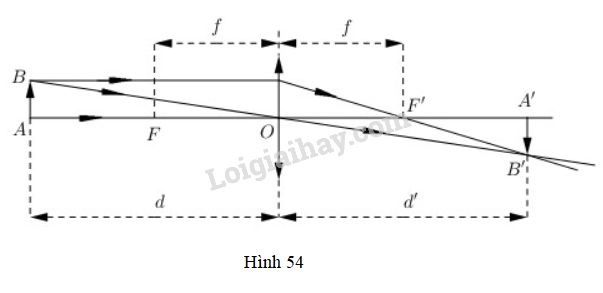
Một thấu kính hội tụ có tiêu cự là f. Gọi d và d′ lần lượt là khoảng cách từ một vật thật AB và từ ảnh A′B′ của nó tới quang tâm O của thấu kính (h.54). Công thức thấu kính là 1d+1d′=1f.
LG a
Tìm biểu thức xác định hàm số d′=φ(d).
Phương pháp giải:
Sử dụng công thức 1d+1d′=1f.
Lời giải chi tiết:
1d+1d′=1f ⇔1d′=1f−1d ⇔1d′=d−ffd ⇔d′=fdd−f
Vậy d′=φ(d)=fdd−f.
LG b
Tìm lim, \underset{d\rightarrow f^{-} }{\lim} φ(d) và \underset{d\rightarrow +\infty }{\lim} φ(d). Giải thích ý nghĩa của các kết quả tìm được.
Phương pháp giải:
Sử dụng quy tắc tìm giới hạn của thương.
Lời giải chi tiết:
\begin{array}{l} + )\,\,\mathop {\lim }\limits_{d \to {f^ + }} \varphi \left( d \right) = \mathop {\lim }\limits_{d \to {f^ + }} \dfrac{{fd}}{{d - f}}\\ \mathop {\lim }\limits_{d \to {f^ + }} \left( {fd} \right) = {f^2} > 0\\ \mathop {\lim }\limits_{d \to {f^ + }} \left( {d - f} \right) = 0;\,\,d \to {f^ + } \Rightarrow d > f \Rightarrow d - f > 0\\ \Rightarrow \mathop {\lim }\limits_{d \to {f^ + }} \varphi \left( d \right) = + \infty \end{array}
Ý nghĩa: Nếu vật thật AB tiến dần về tiêu điểm F sao cho d luôn lớn hơn f thì ảnh của nó dần tới dương vô cực.
\begin{array}{l} + )\,\,\mathop {\lim }\limits_{d \to {f^ - }} \varphi \left( d \right) = \mathop {\lim }\limits_{d \to {f^ - }} \dfrac{{fd}}{{d - f}}\\ \mathop {\lim }\limits_{d \to {f^ - }} \left( {fd} \right) = {f^2} > 0\\ \mathop {\lim }\limits_{d \to {f^ - }} \left( {d - f} \right) = 0;\,\,d \to {f^ - } \Rightarrow d < f \Rightarrow d - f < 0\\ \Rightarrow \mathop {\lim }\limits_{d \to {f^ - }} \varphi \left( d \right) = - \infty \end{array}
Ý nghĩa: Nếu vật thật AB tiến dần về tiêu điểm F sao cho d luôn nhỏ hơn f thì ảnh của nó dần tới âm vô sực.
+) \underset{d\rightarrow +\infty }{\lim} φ(d)
=\underset{d\rightarrow +\infty }{\lim} \dfrac{fd}{d-f}
= \underset{d\rightarrow +\infty }{\lim} \dfrac{f}{1-\dfrac{f}{d}} = f.
Ý nghĩa: Nếu vật thật AB ở xa vô cực so với thấu kính thì ảnh của nó ở ngay trên tiêu diện ảnh (mặt phẳng qua tiêu điểm ảnh F' và vuông góc với trục chính).

