Video hướng dẫn giải
Sử dụng máy tính bỏ túi, hãy tính sinx, cosx với x là các số sau:
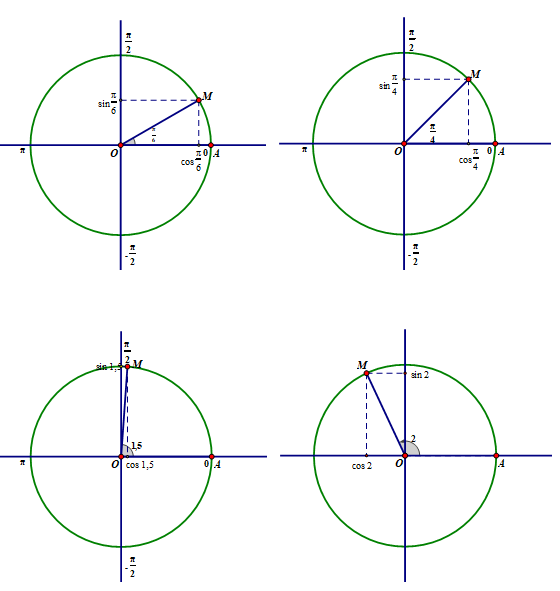
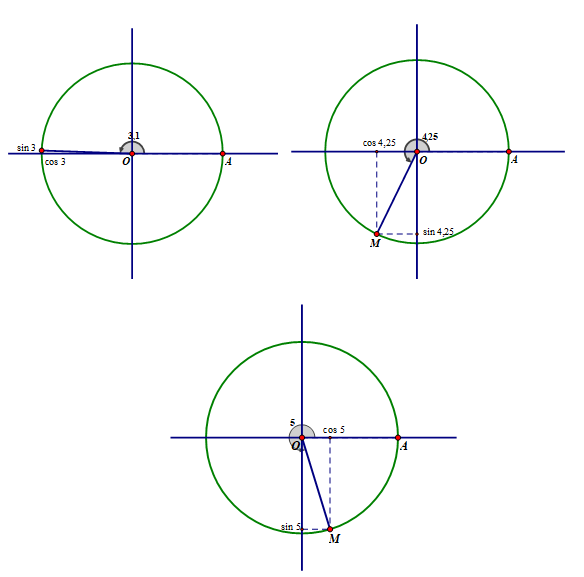
LG a
\(\displaystyle {\pi \over 6};\,{\pi \over 4};\,1,5;\,2;\,3,1;\,4,25;\,5\)
Phương pháp giải:
Nhập các giá trị tương ứng vào hàm sin, cos trên máy tính bỏ túi
Lời giải chi tiết:
\(\begin{array}{l}
\sin \dfrac{\pi }{6} = \dfrac{1}{2};\cos \dfrac{\pi }{6} = \dfrac{{\sqrt 3 }}{2}\\
\sin \dfrac{\pi }{4} = \dfrac{{\sqrt 2 }}{2};{\mkern 1mu} \cos \dfrac{\pi }{4} = \dfrac{{\sqrt 2 }}{2}\\
\sin 1,5 = 0,9975;{\mkern 1mu} \cos 1,5 = 0,0707\\
\sin 2 = 0,9093;{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \cos 2 = - 0,4161\\
\sin 3,1 = 0,0416;{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \cos 3,1 = - 0,9991\\
\sin 4,25 = - 0,8950;{\mkern 1mu} {\mkern 1mu} \cos 4,25 = - 0,4461\\
\sin 5 = - 0,9589;{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \cos 5 = 0,2837
\end{array}\)
LG b
Trên đường tròn lượng giác, với điểm gốc A, hãy xác định các điểm M mà số đo của cung AM bằng x (rad) tương ứng đã cho ở trên và xác định sinx, cosx (lấy π ≈ 3,14)
Lời giải chi tiết: