Video hướng dẫn giải
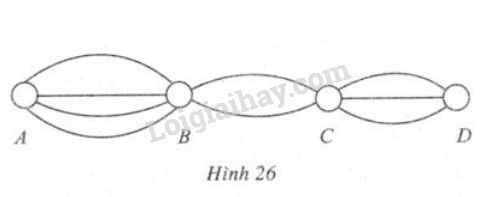
Các thành phố \(A, B, C, D\) được nối với nhau bởi các con đường như hình 26. Hỏi:
LG a
Có bao nhiêu cách đi từ \(A\) đến \(D\) mà qua \(B\) và \(C\) chỉ một lần ?
Phương pháp giải:
Sử dụng quy tắc cộng và quy tắc nhân phù hợp.
Lời giải chi tiết:
Để đi từ \(A\) đến \(D\) mà qua \(B\) và \(C\) chỉ một lần, phải thực hiện liên tiếp ba hành động sau đây:
Hành động 1: Đi từ \(A\) đến \(B\). Có \(4\) cách để thực hiện hành động này.
Hành động 2: Đi từ \(B\) đến \(C\). Có \(2\) cách để thực hiện hành động này.
Hành động 3: Đi từ \(C\) đến \(D\). Có \(3\) cách để thực hiện hành động này.
Theo quy tắc nhân suy ra số các cách để đi từ \(A\) đến \(D\) mà qua \(B\) và \(C\) chỉ một lần là \(4 . 2 . 3 = 24\) (cách).
LG b
Có bao nhiêu cách đi từ \(A\) đến \(D\) rồi quay lại \(A\) ?
Lời giải chi tiết:
Khi đi từ \(A\) đến \(D\) rồi quay về \(A\) nghĩa là công việc được thực hiện qua 2 hành động:
+) Từ \(A\) đến \(D\) qua \(B\), \(C\) chỉ 1 lần có 24 cách.
+) Từ \(D\) về \(A\) qua \(C\), \(B\) chỉ 1 lần có 24 cách.
Áp dụng quy tắc nhân, số các cách để đi từ \(A\) đến \(D\) (mà qua \(B\) và \(C\) chỉ một lần), rồi quay lại \(A\) (mà qua \(C\) và \(B\) chỉ một lần) là:
\(24.24 = 576\) (cách).

