Đề bài
Cho hình lập phương ABCD.A′B′C′D′ cạnh a.
a) Chứng minh rằng B′D vuông góc với mặt phẳng (BA′C′).
b) Tính khoảng cách giữa hai mặt phẳng (BA′C′) và (ACD′).
c) Tính khoảng cách giữa hai đường thẳng BC′ và CD′.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Chứng minh B′D vuông góc với hai đường thẳng cắt nhau trong mp(BA′C′).
b) Chứng minh (BA′C′)//(ACD′). Xác định khoảng cách giữa hai mặt phẳng song song.
c) Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đó.
Lời giải chi tiết
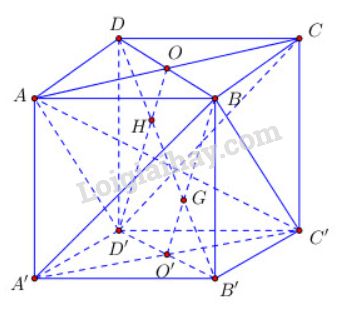
a) Ta có:
BB′⊥(A′B′C′D′)⇒BB′⊥A′C′{A′C′⊥B′D′A′C′⊥BB′⇒A′C′⊥(BB′D′D)⇒A′C′⊥B′DDC⊥(BCC′B′)⇒DC⊥BC′{BC′⊥B′CBC′⊥DC⇒BC′⊥(A′B′CD)⇒BC′⊥B′D{B′D⊥A′C′B′D⊥BC′⇒B′D⊥(BA′C′)
Cách khác:
Ta có B′A′=B′B=B′C′
⇒B′ thuộc trục của tam giác A′BC′ (1)
DA′=DB=DC′ (đường chéo các hình vuông bằng nhau)
⇒D cũng thuộc trục của tam giác A′BC′ (2)
Từ (1) và (2) ⇒B′D là trục của (BA′C′) ⇒B′D⊥(BA′C′).
b) Ta có:
{BC′//AD′A′C′//ACBC′,A′C′⊂(BA′C′)AD′,AC⊂(ACD′)
⇒(BA′C′)//(ACD′)
Mà B′D⊥(BA′C′) nên B′D⊥(ACD′)
Gọi G=B′D∩(BA′C′);H=B′D∩(ACD′)
⇒d((BA′C′);(ACD′))=GH
Gọi O,O′ lần lượt là tâm các hình vuông ABCD,A′B′C′D′ ta có:
BO′//D′O nên O′G//D′H, mà O′ là trung điểm của B′D′⇒G là trung điểm của B′H.
⇒GB′=GH (3)
BO′//D′O nên OH//GB, mà O là trung điểm của BD⇒H là trung điểm của DG.
⇒HG=HD (4)
Từ (3) và (4) suy ra: GB′=GH=HD⇒GH=13B′D
Do ABCD.A′B′C′D′ là hình lập phương cạnh a nên:
B′D=√B′B2+BD2=√B′B2+BA2+AD2=√a2+a2+a2=a√3
⇒HG=a√33.
Vậy d((BA′C′);(ACD′))=a√33.
c) BC′⊂(BA′C′); CD′⊂(ACD′), mà (BA′C′)//(ACD′)
Vậy d(BC′,CD′)=d((BA′C′),(ACD′))=a√33.

