Đề bài
Câu 1. Trong không gian có ba đường thẳng phân biệt a, b, c. Khẳng định nào sau đây sai?
A. Nếu a và b cùng nằm trong một mặt phẳng và cùng vuông góc với c thì \(a \bot b\).
B. Nếu a // b và \(c \bot a\) thì \(c \bot b\).
C. Nếu a , b và c đồng phẳng và a , b cùng vuông góc với c thì a // b.
D. Nếu a // b thì góc giữa a và c bằng góc giữa b và c.
Câu 2. Cho chóp S. ABCD có \(SA \bot \left( {ABCD} \right)\) và đáy là hình vuông . Từ A kẻ \(AM \bot SB\). Khẳng định nào sau đây đúng?
A. \(SB \bot \left( {MAC} \right)\). B. \(AM \bot \left( {SAD} \right)\).
C. \(AM \bot \left( {SBD} \right)\). D. \(AM \bot \left( {SBC} \right)\).
Câu 3. Cho hình chóp S. ABCD có ABCD là hình bình hành tâm O. Trong các mệnh đề sau, mệnh đề nào sai ?
A. \(\overrightarrow {SA} + \overrightarrow {SC} = 2\overrightarrow {SO} \).
B. \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \).
C. \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \).
D. \(\overrightarrow {SA} + \overrightarrow {SB} = \overrightarrow {SC} + \overrightarrow {SD} \).
Câu 4. Cho hình lăng trụ tam giác ABC.A’B’C’. Véc tơ nào sau đây là véc tơ chỉ phương của đường thẳng AB ?
A. \(\overrightarrow {A'C'} \). B. \(\overrightarrow {A'C} \).
C. \(\overrightarrow {A'B'} \). D. \(\overrightarrow {A'B} \).
Câu 5. Cho hình tứ diện ABCD có AB , BC, CD đôi một vuông góc . Điểm cách đều bốn điểm A, B, C, D là:
A. Trung điểm J của AB.
B. Trung điểm I của BC.
C. Trung điểm M của AD.
D. Trung điểm N của CD.
Câu 6. Mệnh đề nào sau đây sai?
A. Hai đường thẳng cùng vuông góc với một mặt phẳng thì song song hoặc trùng nhau.
B. Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.
C. Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.
D. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
Câu 7. Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc với nhau. Khi đó góc giữa AB và CD bằng:
A. 450 B. 600
C. 900 D. 300.
Câu 8. Cho hình chóp S. ABCD có đáy là tam giác đều cạnh a, \(SA \bot (ABC)\,,SA = \dfrac{a}{2}\). Góc giữa hai mặt phẳng (SAB) và (ABC) bằng:
A. 00 B. 450
C. 600 D. 900.
Câu 9. Cho hình chóp tam giác đều S. ABC và đường cao SH, M là trung điểm của BC. \(SA \bot BC\) vì:
\(A. SA \bot (SBC)\,\, \supset \,\,BC\,\,(\,\,SA \bot AM\,\,,\,\,SA \bot NC)\)
\(B. SA \bot (SBC)\,\, \supset \,\,BC\,\,(\,\,SA \bot SB\,\,,\,\,SA \bot SC)\)
\(C. BC \bot (SAM) \supset \,\,SA\,\,(\,\,BC \bot AM\,,\,\,BC \bot SH)\)
\(D. BC \bot (SAM)\,\, \supset \,\,BC\,\,\,\,(do\,BC \bot SH)\)
Câu 10. Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi tâm \(O\) cạnh a, góc nhọn bằng 600 và cạnh \(SC\) vuông góc với mặt phẳng \((ABCD)\) và \(SC =\dfrac{{a\sqrt 6 }}{3}\).Góc giữa hai mặt phẳng \((SBD)\) và \((SAC)\) bằng:
A. 300 B. 450
C. 600 D. 900
Lời giải chi tiết
| Câu | 1 | 2 | 3 | 4 | 5 |
| Đáp án | A | D | D | C | C |
| Câu | 6 | 7 | 8 | 9 | 10 |
| Đáp án | C | C | D | C | D |
Giải
Câu 1. Nếu a và b cùng nằm trong một mặt phẳng và cùng vuông góc với c thì \(a // b\). Chọn đáp án A.
Câu 2.
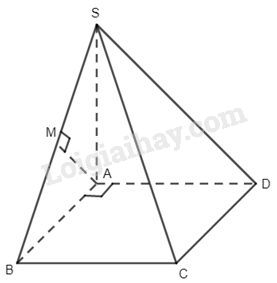
Ta có
\(\begin{array}{l}\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right.\,\, \Rightarrow BC \bot \left( {SAB} \right)\, \Rightarrow BC \bot AM\\AM \bot SB\,\, \Rightarrow \,\,AM \bot \left( {SBC} \right)\end{array}\)
Chọn đáp án D.
Câu 3. Do O là tâm của hình bình hành ABCD nên đáp án A , B đúng.
Do \(\left\{ \begin{array}{l}\overrightarrow {SA} + \overrightarrow {SC} = 2\overrightarrow {SO} \\\overrightarrow {SB} + \overrightarrow {SD} = 2\overrightarrow {SO} \end{array} \right.\,\, \Rightarrow \overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \) suy ra đáp án C đúng.
Chọn đáp án D.
Câu 4.
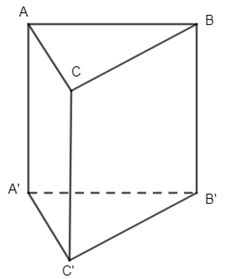
Do AB và A’B’ song song với nhau nên \(\overrightarrow {A'B'} \) là vec tơ chỉ phương của đường thẳng AB. Chọn đáp án C.
Câu 5.
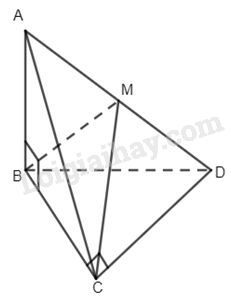
Ta có
\(\begin{array}{l}CD \bot BC,\,\,AB \bot CD\,\, \Rightarrow CD \bot \left( {ABC} \right)\\AB \bot BC,\,\,AB \bot CD\,\, \Rightarrow AB \bot \left( {CBD} \right)\end{array}\) .
Đáp án A sai vì tam giác ABC không vuông góc tại C nên trung điểm của AB không cách đều ba điểm A, B, C.
Đáp án B sai do tam giác BCD không vuông góc tại D nên trung điểm của BC không cách dều ba điểm B, C, D.
Đáp án D sai vì tam giác BCD không vuông góc tại B nên trung điểm của CD không cách đều ba điểm B, C, D.
Đáp án C đúng do tam giác ABD vuông tại B nên M cách đều A, B, D và do tam giác ACD vuông tại C ( do \(CD \bot \left( {ABC} \right)\) ) nên M cách đều A, C, D. từ đó cách đều bốn điểmA, B, C, D.
Câu 7.
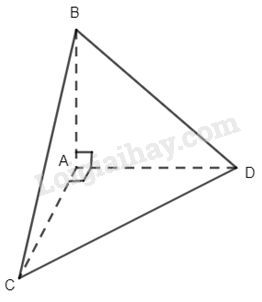
Ta có \(\left\{ \begin{array}{l}AB \bot AC\\AB \bot AD\end{array} \right.\,\, \to AB \bot \left( {CAD} \right)\,\, \Rightarrow AB \bot CD\) .
Do đó, góc giữa AB và CD là 900.
Chọn đáp án C.
Câu 8.
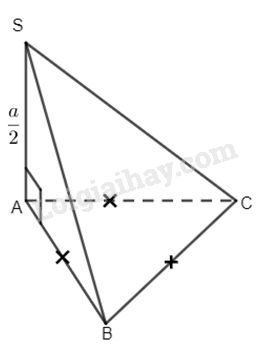
Ta có (SAB) và (ABC) có AB chung và \(\left\{ \begin{array}{l}SA \subset (SAB)\\SA \bot (ABC)\end{array} \right.\,\, \Rightarrow \,\,\left( {SAB} \right) \bot \left( {ABC} \right)\).
Vậy góc giữa hai mặt phẳng trên là 900. Chọn đáp án D.
Câu 9.
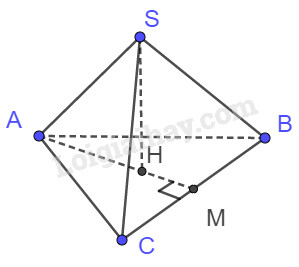
Ta có:
\(SH \bot \left( {ABC} \right) \Rightarrow SH \bot BC\). Mà \(\Delta ABC\) đều nên \(AM \bot BC\).
Suy ra \(BC \bot \left( {SAM} \right) \Rightarrow BC \bot SA\)
Câu 10.
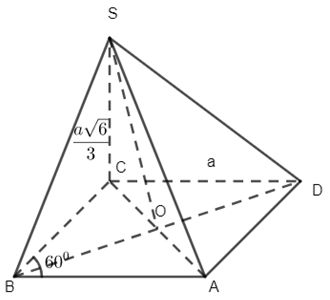
Ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}CA \bot BD\\SC \bot BD\end{array} \right.\,\, \Rightarrow \,\,BD \bot \left( {SAC} \right)\\BD \subset \left( {SBD} \right) \Rightarrow \,\,\left( {SAC} \right) \bot \left( {SBD} \right)\end{array}\)
Vậy góc giữa hai mặt phẳng trên là 900.
Chọn đáp án D.

