Đề bài
Chứng minh rằng sin2(x+kπ)=sin2x với mọi số nguyên k. Từ đó vẽ đồ thị hàm số y=sin2x.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Dựa vào tính tuần hoàn và chu kì của hàm số y=sinx: Hàm y=sinx là hàm tuần hoàn với chu kì 2π.
Lời giải chi tiết
Hàm y=sinx là hàm tuần hoàn với chu kì 2π nên ta có:
sin2(x+kπ)=sin(2x+k2π)=sin2x∀k∈Z
Ta có:
f(x)=sin2x⇒f(x+π)=sin2(x+π)=sin(2x+k2π)=sin2x=f(x)
⇒ Hàm số y=sin2x tuần là hàm tuần hoàn với chu kì π.
Xét hàm số y=sin2x trên đoạn [0;π].
Ta lấy các điểm đặc biệt như sau:
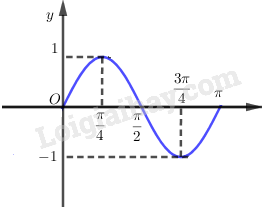
Từ đó ta có đồ thị hàm số y=sin2x trên đoạn [0;π] là:
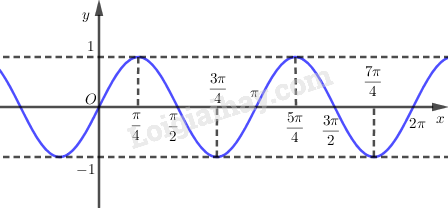
Do hàm số y=sin2x tuần hoàn với chu kì π nên ta có đồ thị là: