Đề bài
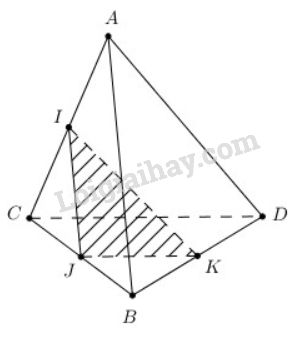
Cho tứ diện ABCD. Gọi I,J và K lần lượt là trung điểm của AC,BC và BD (h.2.75). Giao tuyến của hai mặt phẳng (ABD) và (IJK) là
(A) KD;
(B) KI;
(C) Đường thẳng qua K và song song với AB;
(D) Không có.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng tính chất: Nếu hai mặt phẳng chứa hai đường thẳng song song thì cắt nhau theo giao tuyến song song với hai đường thẳng đó.
Lời giải chi tiết
Ta có: {(ABD)⊃AB(IJK)⊃IJAB//IJK∈(ABC)∩(IJK)
⇒ Giao tuyến của hai mặt phẳng (ABD) và (IJK) là đường thẳng qua K và song song với AB.
Chọn đáp án C.

