Đề bài
Cho bốn điểm A,B,CA,B,C và DD không đồng phẳng. Gọi I,KI,K lần lượt là trung điểm của hai đoạn thẳng ADAD và BCBC
a) Tìm giao tuyến của hai mặt phẳng (IBC)(IBC) và (KAD)(KAD)
b) Gọi MM và NN là hai điểm lần lượt lấy trên hai đoạn thẳng ABAB và ACAC. Tìm giao tuyến của hai mặt phẳng (IBC)(IBC) và (DMN)(DMN).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Chứng minh I,KI,K là hai điểm chung của (BIC)(BIC) và (AKD)(AKD). Từ đó suy ra giao tuyến là IK
b) Tìm hai điểm chung của hai mặt phẳng (IBC)(IBC) và (DMN)(DMN).
Lời giải chi tiết
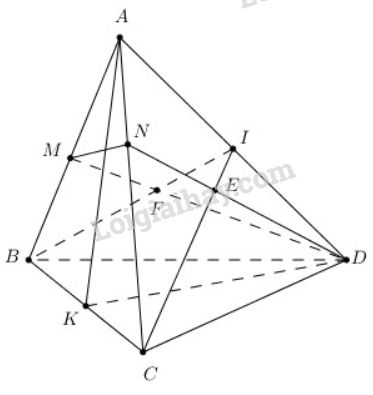
a) Chứng minh I,KI,K là hai điểm chung của (BIC)(BIC) và (AKD)(AKD)
I∈AD⊂(KAD)⇒I∈(KAD)I∈AD⊂(KAD)⇒I∈(KAD)
Mà I∈(BIC)I∈(BIC) ⇒I∈(KAD)∩(IBC)⇒I∈(KAD)∩(IBC)
K∈BC⊂(BIC)⇒K∈(BIC)K∈BC⊂(BIC)⇒K∈(BIC)
Mà K∈(KAD)K∈(KAD) ⇒K∈(KAD)∩(IBC)⇒K∈(KAD)∩(IBC),
Vậy KI=(KAD)∩(IBC)KI=(KAD)∩(IBC)
b) Trong (ACD)(ACD) gọi E=CI∩DNE=CI∩DN
⇒{E∈CI⊂(BIC)E∈DN⊂(DMN)
⇒E∈(IBC)∩(DMN)
Trong (ABD) gọi F=BI∩DM ⇒{F∈BI⊂(BIC)F∈DM⊂(DMN)
⇒F∈(IBC)∩(DMN).
Vậy EF=(IBC)∩(DMN).

