Đề bài
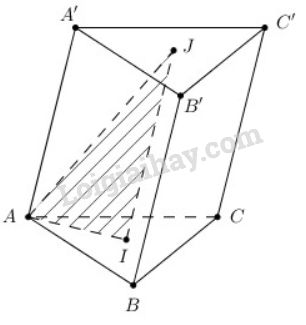
Cho hình lăng trụ tam giác ABC.A′B′C′, Gọi I,J lần lượt là trọng tâm của tam giác ABC và A′B′C′ (h.2.77). Thiết diện tạo bởi mặt phẳng (AIJ) với hình lăng trụ đã cho là
(A) Tam giác cân;
(B) Tam giác vuông;
(C) Hình thang;
(D) Hình bình hành.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Xác định thiết diện của lăng trụ tạo bởi mặt phẳng (AIJ).
Sử dụng tính chất: Nếu hai mặt phẳng chứa hai đường thẳng song song thì cắt nhau theo giao tuyến song song với hai đường thẳng đó.
Lời giải chi tiết
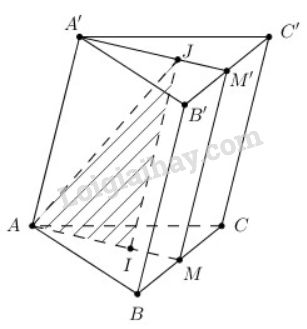
Gọi M,M′ lần lượt là trung điểm của BC,B′C′.
Do I,J là trọng tâm tam giác ABC,A′B′C′ nên A,I,M thẳng hàng và A′,J,M′ thẳng hàng.
Do đó (AA′M′M)≡(AIJ) nên thiết diện của lăng trụ tạo bởi mặt phẳng (AIJ) là tứ giác AA′M′M.
Ta có {(AA′M′M)∩(A′B′C′)=A′M′(AA′M′M)∩(ABC)=AM(ABC)//(A′B′C′)
⇒A′M′//AM.
Lại có ΔABC=ΔA′B′C′⇒AM=A′M′.
Vậy tứ giác AA′M′M là hình bình hành.
Chọn đáp án D.

