Đề bài
I. PHẦN TRẮC NGHIỆM (20 câu - 4,0 điểm – Thời gian: 35 phút)
Câu 1 : Từ các chữ số 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên gồm 3 chữ số?
A. 100. B. 120.
C. 180. D. 216.
Câu 2 : Từ một nhóm học sinh gồm 6 nam, 7 nữ, chọn ngẫu nhiên 3 học sinh. Tính xác suất để trong 3 học sinh được chọn có đúng 2 nam.
A. \(\dfrac{{105}}{{286}}\).
B. \(\dfrac{{27}}{{286}}\).
C. \(\dfrac{{11}}{{143}}\).
D. \(\dfrac{{63}}{{143}}\).
Câu 3 : Cho khai triển \({\left( {x + 2} \right)^n}\). Tìm số hạng chứa \({x^6}\) của khai triển biết \(2C_n^2 + 3A_n^2 - 360 = 0\).
A. 3360.
B. \(3360{x^6}\).
C. \(13440\).
D. \(13440{x^6}\).
Câu 4 : Cho đa giác đều (H) có 16 đỉnh. Chọn ngẫu nhiên 3 đỉnh trong 16 đỉnh của (H). Xác suất để 3 đỉnh được chọn tạo thành một tam giác vuông là.
A. \(\dfrac{1}{{35}}\). B. \(\dfrac{1}{{10}}\).
C. \(\dfrac{1}{5}\). D. \(\dfrac{2}{{35}}\).
Câu 5 : Tìm tập xác định của hàm số \(y = \dfrac{{2\sin x + 1}}{{\cos x - 1}}\).
A. \(D = R{\rm{\backslash }}\left\{ 1 \right\}\).
B. \(D = R{\rm{\backslash }}\left\{ {\dfrac{\pi }{2} + k\pi ,k \in Z} \right\}\).
C. \(D = R{\rm{\backslash }}\left\{ {k\pi ,k \in Z} \right\}\).
D. \(D = R{\rm{\backslash }}\left\{ {k2\pi ,k \in Z} \right\}\).
Câu 6 : Phương trình \(\sin \,x + \sqrt 3 \cos x = 2\) tương đương với phương trình nào sau đây?
A. \(\sin \left( {x + \dfrac{\pi }{3}} \right) = 1\).
B. \(\sin \left( {x - \dfrac{\pi }{3}} \right) = 1\).
C. \(\cos \left( {x + \dfrac{\pi }{3}} \right) = 1\).
D. \(\cos \left( {x - \dfrac{\pi }{3}} \right) = 1\).
Câu 7 : Tìm nghiệm của phương trình \(\cot \left( {x - \dfrac{\pi }{3}} \right) = \dfrac{{\sqrt 3 }}{3}\).
A. \(x = \dfrac{\pi }{3} + k\pi ,k \in Z\).
B. \(x = \dfrac{\pi }{2} + k2\pi ,k \in Z\).
C. \(x = \dfrac{{2\pi }}{3} + k\pi ,k \in Z\).
D. \(x = k\pi ,k \in Z\).
Câu 8 : Gọi S là tổng các nghiệm của phương trình \(\left( {7 - 2\cos 2x} \right)\left( {{{\sin }^4}x - {{\cos }^4}x} \right) + 3 = 0\) trong khoảng \(\left( { - \pi ;\pi } \right)\). Giá trị của S là:
A. \(S = 0\).
B. \(S = \dfrac{{5\pi }}{3}\).
C. \(S = 2\pi \).
D. \(S = 4\pi \).
Câu 9 : Cho tam giác ABC có trọng tâm G, gọi I là trung điểm của BC. Trong các mệnh đề dưới đây mệnh đề nào SAI?
A. Phép vị tự tâm A tỉ số \(k = \dfrac{3}{2}\) biến điểm G thành điểm I.
B. Phép vị tự tâm I tỉ số \(k = \dfrac{1}{3}\) biến điểm A thành điểm G.
C. Phép vị tự tâm A tỉ số \(k = \dfrac{2}{3}\) biến điểm I thành điểm G.
D. Phép vị tự tâm I tỉ số \(k = \dfrac{1}{3}\) biến điểm G thành điểm A.
Câu 10 : Trong mặt phẳng Oxy, phép quay tâm O góc \( - 90^\circ \) biến điểm \(M\left( {2;1} \right)\) thành điểm N. Tìm tọa độ của điểm N.
A. \(N\left( {1; - 2} \right)\).
B. \(N\left( {1;2} \right)\).
C. \(N\left( { - 1;2} \right)\).
D. \(N\left( { - 1; - 2} \right)\).
Câu 11 : Trong mặt phẳng Oxy, gọi \(B = \left( { - 1;2} \right)\) là ảnh của điểm A qua phép tịnh tiến theo vecto \(\overrightarrow u = \left( { - 3;1} \right)\). Tìm tọa độ của điểm A.
A. \(A = \left( { - 2;1} \right)\).
B. \(A = \left( { - 4;3} \right)\).
C. \(A = \left( {2;1} \right)\).
D. \(A = \left( {2; - 1} \right)\).
Câu 12 : Trong mặt phẳng Oxy, cho đường tròn (C) có bán kính bằng 8. Gọi đường tròn (C’) là ảnh của (C) qua phép vị tự tỉ số k = - 2. Tính bán kính R’ của đường tròn (C’).
A. \(R' = 8\).
B. \(R' = 16\).
C. \(R' = - 16\).
D. \(R' = 4\).
Câu 13 : Trong mặt phẳng Oxy, gọi đường thẳng (d) là ảnh của đường thẳng \(\left( \Delta \right):2x - y + 3 = 0\) qua phép tịnh tiến theo vecto \(\overrightarrow u = \left( {3;2} \right)\). Tìm phương trình đường thẳng (d).
A. \(2x - y + 7 = 0\).
B. \(2x - y + 3 = 0\).
C. \( - 2x + y - 1 = 0\).
D. \( - 2x + y + 1 = 0\).
Câu 14 : Cho dãy số \(\left( {{u_n}} \right):\left\{ \begin{array}{l}{u_1} = 1,\,{u_2} = 1\\{u_n} = {u_{n - 1}} + 2{u_{n - 2}},\,\,\left( {n \ge 3,n \in N} \right)\end{array} \right.\). Giá trị \({u_4} + {u_5}\) là:
A. 16. B. 20.
C. 22. D. 24.
Câu 15 : Dãy số \(\left( {{u_n}} \right)\)nào có công thức tổng quát dưới đây là dãy số tăng?
A. \({u_n} = {\left( { - 1} \right)^n}\left( {3 + {2^n}} \right)\).
B. \({u_n} = \cos n\).
C. \({u_n} = {\left( {\dfrac{3}{2}} \right)^n}\).
D. \({u_n} = 1 - 2n\).
Câu 16 : Cho cấp số cộng có số hạng đầu \({u_1} = 2\) và có công sai \(d = - 3\). Mệnh đề nào sau đây sai?
A. \({u_{10}} = - 25\).
B. \({u_{15}} = - 40\).
C. \({u_{25}} = - 75\).
D. \({u_{26}} = - 73\).
Câu 17 : Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_2} + {u_{29}} = 40\). Giá trị của \({S_{30}} = {u_1} + {u_2} + ... + {u_{30}}\) là:
A. 640. B. 600.
C. 620. D. 500.
Câu 18 : Có bao nhiêu số tự nhiên nhỏ hơn 151 và chia hết cho 3?
A. 49. B. 50.
C. 51. D. 52.
Câu 19 : Cho mặt phẳng (P) và điểm A không thuộc (P). Số đường thẳng qua A song song (P) là:
A. 0. B. 1.
C. 2. D. Vô số.
Câu 20 : Cho hình chóp S.ABCD có ABCD là hình thang (AB // CD). M là trung điểm của SC. Giao điểm của mặt phẳng (ABM) và mặt phẳng (SCD) là đường thẳng d. Mệnh đề nào sau đây là đúng?
A. d đi qua M và song song đường thẳng SA.
B. d đi qua M và cắt đường thẳng SB.
C. d đi qua M và song song đường thẳng CD.
D. d đi qua M và cắt đường thẳng AB.
II. PHẦN TỰ LUẬN (6,0 điểm – 55 phút)
Câu 1: (2,0 điểm) . Giải các phương trình sau:
a) \(2\sin x - 1 = 0\).
b) \({\sin ^2}x - \cos x + 1 = 0\)
c) \(\sin \,x - \sqrt 3 \cos x = 1\).
Câu 2: (1,5 điểm)
a) Một lớp học gồm 16 học sinh nam và 14 học sinh nữ. Giáo viên chủ nhiệm chọn ngẫu nhiên 6 học sinh để tham gia lớp học về “AN TOÀN GIAO THÔNG”. Tính xác suất để trong 6 học sinh được chọn số học sinh nữ gấp đôi số học sinh nam?
b) Giải phương trình: \(3A_{x - 2}^2 - 2C_x^{x - 2} - 2{x^2} + 38 = 0\)
Câu 3: (2,0 điểm)
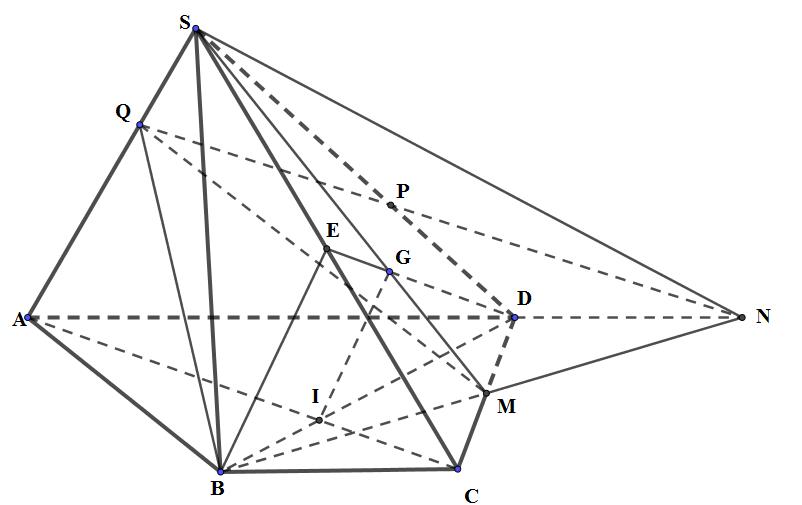
Cho hình chóp S.ABCD có đáy ABCD là hình thang, AD song song BC và AD = 2BC. M là trung điểm của cạnh CD, Q là điểm trên cạnh SA sao cho SA = 3SQ.
a) Xác định giao tuyến của hai mặt phẳng (SAD) và (SBM).
b) Gọi G là trọng tâm tam giác SCD, I là giao điểm của AC và BD. Chứng minh IG // (SBC).
c) Mặt phẳng (BMQ) cắt cạnh SD tại P. Tính tỉ số \(\dfrac{{SP}}{{SD}}\).
Câu 4: (0,5 điểm)
Tìm tất cả các giá trị của tham số m để phương trình \(\sin 2x + m\cos x - 4\sin \,x - 2m = 0\) có nghiệm.
Lời giải chi tiết
I. PHẦN TRẮC NGHIỆM (20 câu - 4,0 điểm – Thời gian: 35 phút)
| 1. D | 2. A | 3. B | 4. C | 5. D |
| 6. A | 7. C | 8. A | 9. D | 10. A |
| 11. C | 12. B | 13. D | 14. A | 15. C |
| 16. C | 17. B | 18. C | 19. D | 20. C |
II. PHẦN TỰ LUẬN (6,0 điểm – 55 phút)
Câu 1: (2,0 điểm). Giải các phương trình sau:
a)
\(2\sin x - 1 = 0 \Leftrightarrow \sin \,x = {1 \over 2}\)
\(\Leftrightarrow \left[ \matrix{
x = {\pi \over 6} + k2\pi \hfill \cr
x = \pi - {\pi \over 6} + k2\pi \hfill \cr} \right. \)
\(\Leftrightarrow \left[ \matrix{
x = {\pi \over 6} + k2\pi \hfill \cr
x = {{5\pi } \over 6} + k2\pi \hfill \cr} \right.\,\,\,\left( {k \in Z} \right)\)
Vậy tập nghiệm của phương trình là: \(S = \left\{ {\dfrac{\pi }{6} + k2\pi ,\,\,\dfrac{{5\pi }}{6} + k2\pi ;\,k \in Z} \right\}\).
b) \({\sin ^2}x - \cos x + 1 = 0 \)
\(\Leftrightarrow 1 - {\cos ^2}x - \cos x + 1 = 0\)
\( \Leftrightarrow - {\cos ^2}x - \cos x + 2 = 0\)
\(\Leftrightarrow \left[ \matrix{
\cos x = 1 \hfill \cr
\cos x = - 2\left( \text{vô nghiệm} \right) \hfill \cr} \right. \)
\(\Leftrightarrow x = k2\pi \,\,\,\left( {k \in Z} \right)\)
Vậy phương trình có tập nghiệm là: \(S = \left\{ {k2\pi ;\,k \in Z} \right\}\).
c) \(\sin \,x - \sqrt 3 \cos x = 1\)
\(\Leftrightarrow {1 \over 2}\sin \,x - {{\sqrt 3 } \over 2}\cos x = {1 \over 2}\)
\(\eqalign{
& \Leftrightarrow \cos {\pi \over 3}\sin \,x - \sin {\pi \over 3}\cos x = {1 \over 2}\cr& \Leftrightarrow \sin \,\left( {x - {\pi \over 3}} \right) = {1 \over 2} \cr
& \Leftrightarrow \left[ \matrix{
x - {\pi \over 3} = {\pi \over 6} + k2\pi \hfill \cr
x - {\pi \over 3} = \pi - {\pi \over 6} + k2\pi \hfill \cr} \right. \cr&\Leftrightarrow \left[ \matrix{
x = {\pi \over 2} + k2\pi \hfill \cr
x = {{7\pi } \over 6} + k2\pi \hfill \cr} \right.\,\,\left( {k \in Z} \right) \cr} \)
Vậy tập nghiệm của phương trình là: \(S = \left\{ {\dfrac{\pi }{2} + k2\pi ,\dfrac{{7\pi }}{6} + k2\pi ;\,k \in Z} \right\}\).
Câu 2: (1,5 điểm)
Số phần tử của không gian mẫu: \(n\left( \Omega \right) = C_{16 + 14}^6 = C_{30}^6\)
Gọi A: “trong 6 học sinh được chọn số học sinh nữ gấp đôi số học sinh nam”
Vì trong 6 học sinh được chọn số học sinh nữ gấp đôi số học sinh nam nên số học sinh nam là 2, số học sinh nữ là 4.
\(\Rightarrow n\left( A \right) = C_{16}^2C_{14}^4\)
\( \Rightarrow P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \dfrac{{C_{16}^2C_{14}^4}}{{C_{30}^6}} = \dfrac{{88}}{{435}}\)
b) Giải phương trình: \(3A_{x - 2}^2 - 2C_x^{x - 2} - 2{x^2} + 38 = 0\)
\(3A_{x - 2}^2 - 2C_x^{x - 2} - 2{x^2} + 38 = 0,\)\(\left( {x \in N,x \geqslant 4} \right)\)
\(\begin{array}{l} \Leftrightarrow 3.\dfrac{{\left( {x - 2} \right)!}}{{\left( {x - 4} \right)!}} - 2.\dfrac{{x!}}{{\left( {x - 2} \right)!2!}}\\ - 2{x^2} + 38 = 0\\ \Leftrightarrow 3\left( {x - 2} \right)\left( {x - 3} \right) - x\left( {x - 1} \right)\\ - 2{x^2} + 38 = 0\\ \Leftrightarrow 3{x^2} - 15x + 18 - {x^2} + x\\ - 2{x^2} + 38 = 0\\ \Leftrightarrow - 14x + 56 = 0 \Leftrightarrow x = 4\left( {tm} \right)\end{array}\)
Phương trình có tập nghiệm \(S = \left\{ 4 \right\}\).
Câu 3:
a) Trong (ABCD) gọi N là giao điểm của AD và BM.
Khi đó, \(\left( {SAD} \right) \cap \left( {SBM} \right) = SN\).
b) Gọi E là trung điểm của SC.
Do G là trọng tâm tam giác SCD nên \(\dfrac{{EG}}{{GD}} = \dfrac{1}{2}\)
Ta có: \(AD//BC,\,\,I = AC \cap BD\,\,\)\( \Rightarrow \dfrac{{IB}}{{ID}} = \dfrac{{BC}}{{AD}} = \dfrac{1}{2}\)
\( \Rightarrow \dfrac{{EG}}{{GD}} = \dfrac{{IB}}{{ID}} = \dfrac{1}{2}\,\, \Rightarrow IG//BE\)
Mà \(BE \subset \left( {SBC} \right) \Rightarrow IG//\left( {SBC} \right)\).
c) Ta có: \(DN//BC,\,\,DC \cap BN = M\)
\(\Rightarrow \dfrac{{DN}}{{BC}} = \dfrac{{DM}}{{MC}} = 1\)
\(\Rightarrow DN = BC \Rightarrow DN = \dfrac{1}{2}AD\)
\(\Rightarrow \dfrac{{DN}}{{AN}} = \dfrac{1}{3}\)
Mà SA = 3SQ \( \Rightarrow \dfrac{{SQ}}{{SA}} = \dfrac{1}{3} \)
\(\Rightarrow \dfrac{{DN}}{{AN}} = \dfrac{{SQ}}{{SA}} = \dfrac{1}{3} \)
\(\Rightarrow \left\{ \begin{gathered}
QD//SN \hfill \\
\frac{{QN}}{{SD}} = \frac{2}{3} \hfill \\
\end{gathered} \right.\)
Do \(DQ//SN,\,\,\,QN \cap SD = P\,\,\,\)\( \Rightarrow \dfrac{{PD}}{{SP}} = \dfrac{{QD}}{{SN}} = \dfrac{2}{3} \Rightarrow \dfrac{{SP}}{{SD}} = \dfrac{3}{5}\)
Câu 4: (0,5 điểm)
\(\begin{array}{l}\sin 2x + m\cos x - 4\sin x - 2m = 0\\ \Leftrightarrow 2\sin x\cos x - 4\sin x\\ + m\cos x - 2m = 0\\ \Leftrightarrow 2\sin x\left( {\cos x - 2} \right) \\+ m\left( {\cos x - 2} \right) = 0\\ \Leftrightarrow \left( {\cos x - 2} \right)\left( {2\sin x + m} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}\cos x = 2(VN)\\\sin x = - \dfrac{m}{2}\end{array} \right. \Leftrightarrow \sin x = - \dfrac{m}{2}\end{array}\)
Phương trình đã cho có nghiệm khi và chỉ khi \( - 1 \le - {m \over 2} \le 1 \Leftrightarrow - 2 \le m \le 2\).
Xem lời giải chi tiết đề thi học kì 1 tại Tuyensinh247.com

