Đề bài
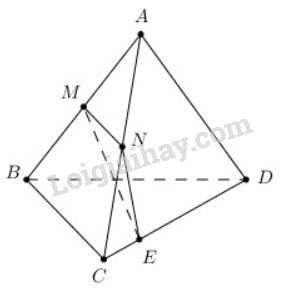
Cho tứ diện ABCDABCD. Gọi MM và NN lần lượt là trung điểm của ABAB và ACAC (h.2.76), EE là điểm trên cạnh CDCD với ED=3ECED=3EC. Thiết diện tạo bởi mặt phẳng (MNE)(MNE) và tứ diện ABCDABCD là:
(A) Tam giác MNEMNE;
(B) Tứ giác MNEFMNEF với FF là điểm bất kì trên cạnh BDBD;
(C) Hình bình hành MNEFMNEF với FF là điểm trên cạnh BDBD mà EF//BCEF//BC;
(D) Hình thang MNEFMNEF với FF là điểm trên cạnh BDBD mà EF//BCEF//BC.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng tính chất: Nếu hai mặt phẳng chứa hai đường thẳng song song thì cắt nhau theo giao tuyến song song với hai đường thẳng đó.
Lời giải chi tiết
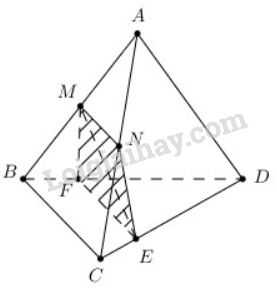
Ta có: MNMN là đường trung bình của tam giác ABC⇒MN//BCABC⇒MN//BC.
{(BCD)⊃BC(MNE)⊃MNMN//BCE∈(MNE)∩(BCD)
⇒ giao tuyến của hai mặt phẳng (MNE) và (BCD) là đường thẳng qua E và song song với BC.
Đường thẳng này cắt BD tại F. Do đó MN//EF//BC.
Ta có MN=12BC.
Áp dụng định lí Ta-let trong tam giác BCD ta có: EFBC=DEDC=34 ⇒EF=34BC⇒MN≠EF.
Vậy MNEF là hình thang.
Chọn đáp án D.

