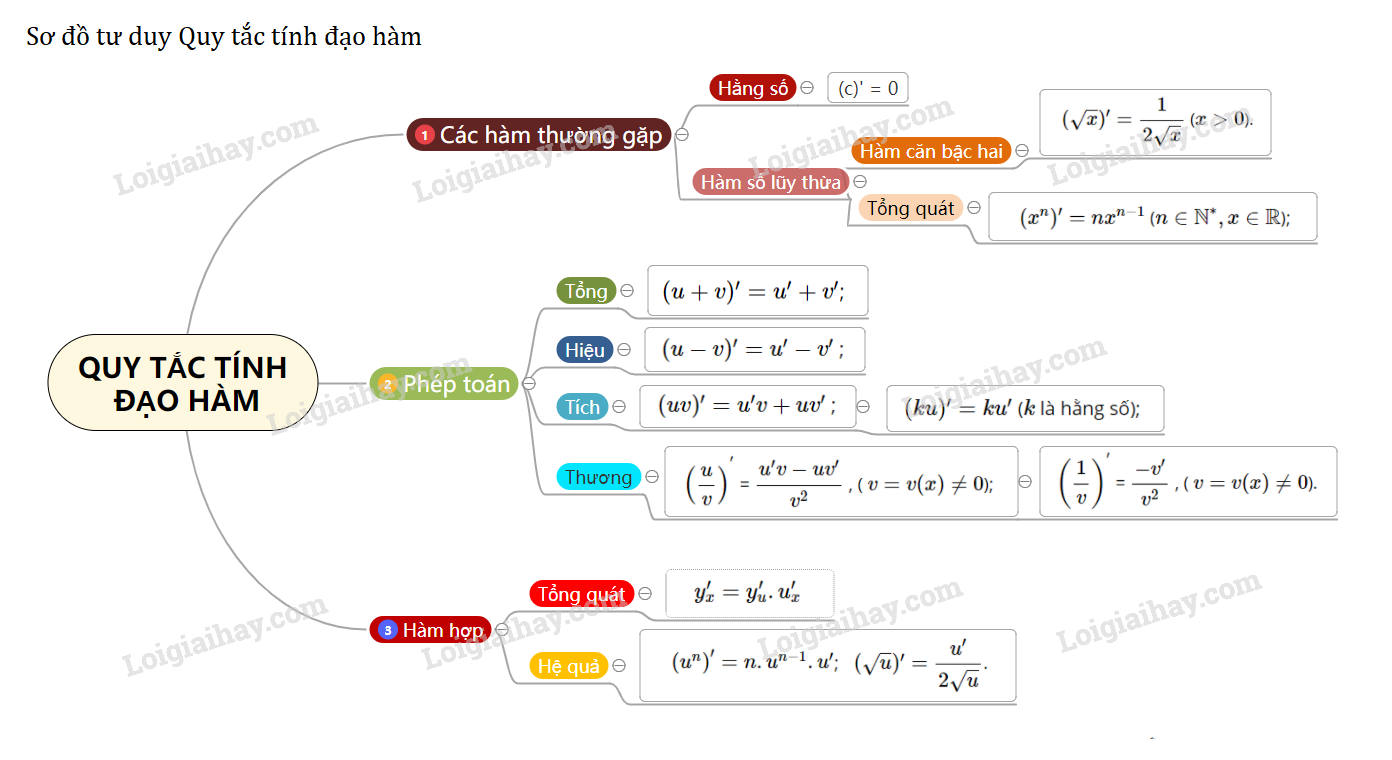
1. Công thức
\((c)' = 0\) ( \(c\) là hằng số);
\((x^n)' = nx^{n-1}\) (\(n\in {\mathbb N}^*, x ∈\mathbb R\));
\((\sqrt x)' = \dfrac{1}{2\sqrt{x}}\) (\(x > 0\)).
2. Phép toán
\((u + v)' = u' + v' \);
\((u - v)' = u' - v'\) ;
\((uv)' = u'v + uv'\) ;
\((ku)' = ku'\) (\(k\) là hằng số);
\( \left ( \dfrac{u}{v} \right )^{^{'}}\) = \( \dfrac{u'v - uv'}{v^{2}}\) , ( \(v = v(x) ≠ 0\));
\( \left ( \dfrac{1}{v} \right )^{'}\) = \( \dfrac{-v'}{v^{2}}\) , ( \(v = v(x) ≠ 0\)).
3. Đạo hàm của hàm hợp
\[y_x' = y_u'.u_x'\]
Hệ quả: +) \(\left( {{u^n}} \right)' = n.{u^{n - 1}}.u'\);
+) \((\sqrt u)' = \dfrac{u'}{2\sqrt{u}}\).