Đề bài
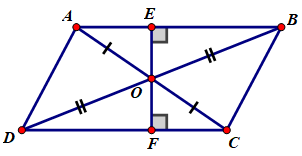
Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo. Đường thẳng kẻ qua O vuông góc với AB, cắt AB ở E và cắt CD ở F. Hãy chỉ ra các cặp điểm trên hình vẽ đối xứng với nhau qua tâm O.
Video hướng dẫn giải
Lời giải chi tiết
- Hình bình hành ABCD có O là giao điểm của hai đường chéo ⇒O là trung điểm mỗi đường nên A và C đối xứng nhau qua tâm O.
B và D đối xứng nhau qua tâm O
- Xét hai tam giác vuông AEO và CFO có:
OA=OC (do O là trung điểm AC)
∠(AOE)=∠(COF) (hai góc đối đỉnh)
⇒ΔAEO=ΔCFO (cạnh huyền – góc nhọn kề)
⇒OE=OF(hai cạnh tương ứng)
Nên O là trung điểm EF
⇒E và F đối xứng nhau qua tâm O.