Đề bài
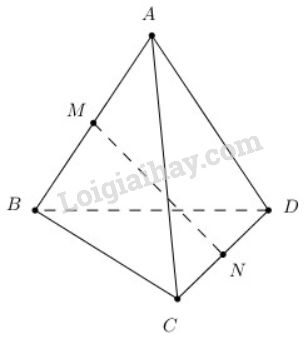
Cho hình tứ diện \(ABCD\). Gọi \(M\) và \(N\) lần lượt là trung điểm của \(AB\) và \(CD\). Chứng minh rằng:
a) \(\overrightarrow{MN}=\dfrac{1}{2}\left ( \overrightarrow{AD}+\overrightarrow{BC} \right );\)
b) \(\overrightarrow{MN}=\dfrac{1}{2}\left ( \overrightarrow{AC}+\overrightarrow{BD} \right ).\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng quy tắc ba điểm.
Lời giải chi tiết
a) \(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AD}+\overrightarrow{DN}.\)
\(\overrightarrow{MN}=\overrightarrow{MB}+\overrightarrow{BC}+\overrightarrow{CN}.\)
Cộng từng vế ta được:
\(\begin{array}{l}
2\overrightarrow {MN} \\
= \left( {\overrightarrow {MA} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {AD} + \overrightarrow {BC} } \right) + \left( {\overrightarrow {DN} + \overrightarrow {CN} } \right)
\end{array}\)
Do \(M,N\) là trung điểm của \(AB,CD\) nên \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 \) và \(\overrightarrow {DN} + \overrightarrow {CN} = \overrightarrow {DN} + \overrightarrow {ND} = \overrightarrow 0 \)
\(\Rightarrow 2\overrightarrow {MN} = \overrightarrow 0 + \left( {\overrightarrow {AD} + \overrightarrow {BC} } \right) + \overrightarrow 0 \) \(= \overrightarrow {AD} + \overrightarrow {BC} \)
\(\Rightarrow \overrightarrow{MN}=\dfrac{1}{2}\left ( \overrightarrow{AD}+\overrightarrow{BC} \right )\)
b)
\(\eqalign{
& \overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AC} + \overrightarrow {CN} \cr
& \overrightarrow {MN} = \overrightarrow {MB} + \overrightarrow {BD} + \overrightarrow {DN} \cr} \)
Cộng từng vế ta được:
\(\begin{array}{l}
2\overrightarrow {MN} \\
= \left( {\overrightarrow {MA} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {AC} + \overrightarrow {BD} } \right) + \left( {\overrightarrow {CN} + \overrightarrow {DN} } \right)\\
= \overrightarrow 0 + \left( {\overrightarrow {AC} + \overrightarrow {BD} } \right) + \overrightarrow 0 \\
= \overrightarrow {AC} + \overrightarrow {BD}
\end{array}\)
\(\Rightarrow \overrightarrow{MN}=\dfrac{1}{2}\left ( \overrightarrow{AC}+\overrightarrow{BD} \right ).\)

