1. Lý thuyết

2. Ví dụ
Tìm và biểu diễn các nghiệm của phương trình sau trên đường tròn lượng giác:
a) \(\sin \left( {2x + \dfrac{\pi }{3}} \right) = \dfrac{1}{2}\)\( \Leftrightarrow \left[ \begin{array}{l}2x + \dfrac{\pi }{3} = \dfrac{\pi }{6} + k2\pi \\2x + \dfrac{\pi }{3} = \dfrac{{5\pi }}{6} + k2\pi \end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{\pi }{{12}} + k\pi \\x = \dfrac{\pi }{4} + k\pi \end{array} \right.,k \in \mathbb{Z}\).
Biểu diễn nghiệm trên đường tròn đơn vị:
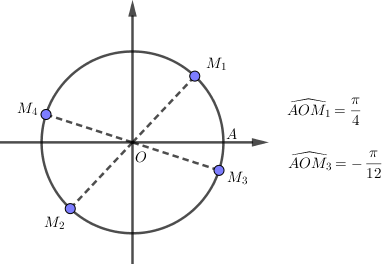
Ở đó, hai điểm \({M_1},{M_2}\) biểu diễn góc \(x = \dfrac{\pi }{4} + k\pi \) và hai điểm \({M_3},{M_4}\) biểu diễn góc \(x = - \dfrac{\pi }{{12}} + k\pi \).
b) \(\dfrac{{2\cos 2x}}{{1 - \sin 2x}} = 0\)
Điều kiện: \(1 - \sin 2x \ne 0 \Leftrightarrow \sin 2x \ne 1\) \( \Leftrightarrow 2x \ne \dfrac{\pi }{2} + k2\pi \Leftrightarrow x \ne \dfrac{\pi }{4} + k\pi \).
Phương trình \( \Leftrightarrow \cos 2x = 0 \Leftrightarrow 2x = \dfrac{\pi }{2} + k\pi \) \( \Leftrightarrow x = \dfrac{\pi }{4} + \dfrac{{k\pi }}{2}\).
Biểu diễn trên đường tròn đơn vị:
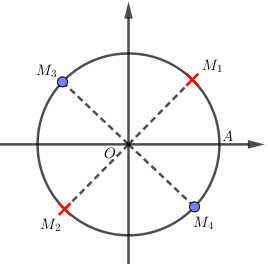
Các điểm biểu diễn \(x = \dfrac{\pi }{4} + k\pi \) là \({M_1},{M_2}\) nhưng điều kiện là \(x \ne \dfrac{\pi }{4} + k\pi \) nên hai điểm này không lấy.
Các điểm biểu diễn \(x = \dfrac{\pi }{4} + \dfrac{{k\pi }}{2}\) là \({M_1},{M_2},{M_3},{M_4}\) nhưng do không lấy hai điểm \({M_1},{M_2}\) nên các điểm biểu diễn nghiệm chỉ còn \({M_3},{M_4}\).
Dễ thấy hai điểm này đối xứng nhau qua \(O\) và \(\widehat {AO{M_4}} = - \dfrac{\pi }{4}\) nên nghiệm của phương trình là \(x = - \dfrac{\pi }{4} + k\pi ,k \in \mathbb{Z}\).
c) \(\dfrac{{\sqrt 3 \cot 2x - 1}}{{2\cos x + 1}} = 0\)
Điều kiện: \(2\cos x + 1 \ne 0 \Leftrightarrow \cos x \ne - \dfrac{1}{2}\) \( \Leftrightarrow \left\{ \begin{array}{l}x \ne \dfrac{{2\pi }}{3} + k2\pi \\x \ne - \dfrac{{2\pi }}{3} + k2\pi \end{array} \right.,k \in \mathbb{Z}\).
Khi đó phương trình \( \Leftrightarrow \sqrt 3 \cot 2x - 1 = 0 \Leftrightarrow \cot 2x = \dfrac{1}{{\sqrt 3 }}\) \( \Leftrightarrow \cot 2x = \cot \dfrac{\pi }{3} \Leftrightarrow 2x = \dfrac{\pi }{3} + k\pi \) \( \Leftrightarrow x = \dfrac{\pi }{6} + \dfrac{{k\pi }}{2},k \in \mathbb{Z}\).
Biểu diễn trên đường tròn đơn vị:
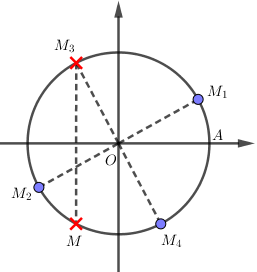
Ở đó, điểm \(M\) biểu diễn góc \(x = \dfrac{{2\pi }}{3} + k2\pi \) và điểm \({M_3}\) biểu diễn góc \(x = - \dfrac{{2\pi }}{3} + k2\pi \), ta đánh dấu đỏ thể hiện không lấy hai điểm đó (do điều kiện xác định).
Các điểm \({M_1},{M_2},{M_3},{M_4}\) là các điểm biểu diễn nghiệm \(x = \dfrac{\pi }{6} + \dfrac{{k\pi }}{2}\), trong đó không lấy điểm \({M_3}\) do điều kiện xác định.
Do đó, chỉ còn lại hai điểm \({M_1},{M_2}\) (với \(\widehat {AO{M_1}} = \dfrac{\pi }{6}\)) biểu diễn góc \(x = \dfrac{\pi }{6} + k\pi \) và điểm \({M_4}\) biểu diễn góc \(x = - \dfrac{\pi }{3} + k2\pi \) (với \(\widehat {AO{M_4}} = - \dfrac{\pi }{3}\)).
Vậy phương trình có nghiệm \(x = \dfrac{\pi }{6} + k\pi \) hoặc \(x = - \dfrac{\pi }{3} + k2\pi \) với \(k \in \mathbb{Z}\).

