Đề bài
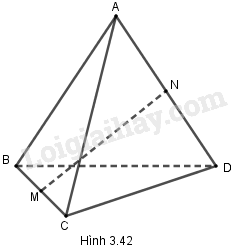
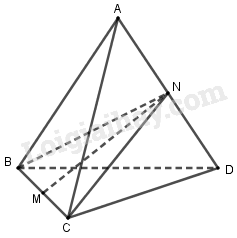
Cho tứ diện đều \(ABCD\). Gọi \(M, N\) lần lượt là trung điểm của cạnh \(BC\) và \(AD\). Chứng minh rằng: \(MN ⊥ BC\) và \(MN ⊥ AD\) (h.3.42)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng tính chất của tứ diện đều và các tam giác đều trong hình, kết hợp tính chất đường thẳng vuông góc với mặt phẳng.
Lời giải chi tiết
Tứ diện đều \(ABCD\) nên các mặt của tứ diện là các tam giác đều bằng nhau
\(NB = NC\) vì là trung tuyến của hai tam giác đều bằng nhau
\(⇒ ΔBNC\) cân tại \(N\)
\(NM\) là đường trung tuyến của tam giác cân \(BNC\)
\(⇒ MN ⊥ BC\)
Lại có: Các tam giác \(ABD, ACD\) đều nên \(CN ⊥ AD\) và \(BN ⊥ AD.\)
Từ đó \(AD ⊥ (BNC)\) hay \(AD ⊥ MN.\)
Vậy ta có điều phải chứng minh.