Đề bài
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a.
a) Hãy xác định đường vuông góc chung của hai đường thẳng chéo nhau BD′ và B′C.
b)Tính khoảng cách của hai đường thẳng BD′ và B′C
Video hướng dẫn giải
Lời giải chi tiết
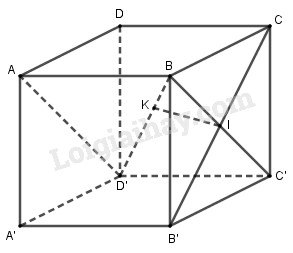
a) AB⊥(BCC′B′)⇒AB⊥B′C
BCC′B′ là hình vuông có BC′⊥B′C
⇒B′C⊥(ABC′D′)
Trong mặt phẳng (ABC′D′), kẻ IK⊥BD′.
Vì B′C⊥(ABC′D′)⇒B′C⊥IK
Kết hợp với IK⊥BD′ ⇒IK là đường vuông góc chung của B′C và BD′
b) Ta có: d(B′C,BD′)=IK
C′B=√CB2+B′B2 =√a2+a2=a√2
D′B=√C′B2+C′D′2 =√2a2+a2=a√3
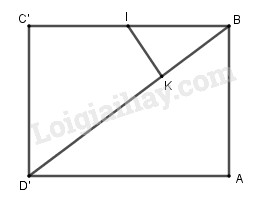
Xét ∆BIK và ∆BD’C’ có:
B chung
\widehat {BC'D'} = \widehat {BKI} = {90^0}
Suy ra ∆BIK \backsim ∆BD’C’ (g-g)
\eqalign{ & \Rightarrow {{IK} \over {D'C'}} = {{BI} \over {B{\rm{D}}'}} \cr & \Rightarrow IK = {{BI.D'C'} \over {B{\rm{D}}'}} \cr} .
Mà BI = \dfrac{1}{2}BC' = \dfrac{{a\sqrt 2 }}{2} nên:
IK = \dfrac{{\frac{{a\sqrt 2 }}{2}.a}}{{a\sqrt 3 }} = \dfrac{{a\sqrt 6 }}{6}
Vậy d\left( {B'C,BD'} \right) = \dfrac{{a\sqrt 6 }}{6}
loigiaihay.com

