Đề bài
Trong mặt phẳng (α)(α) cho tam giác ABCABC vuông ở BB. Một đoạn thẳng ADAD vuông góc với (α)(α) tại AA. Chứng minh rằng:
a) ^ABDˆABD là góc giữa hai mặt phẳng (ABC)(ABC) và (DBC)(DBC);
b) Mặt phẳng (ABD)(ABD) vuông góc với mặt phẳng (BCD)(BCD);
c) HK//BCHK//BC với HH và KK lần lượt là giao điểm của DBDB và DCDC với mặt phẳng (P)(P) đi qua AA và vuông góc với DBDB.
Video hướng dẫn giải
Lời giải chi tiết
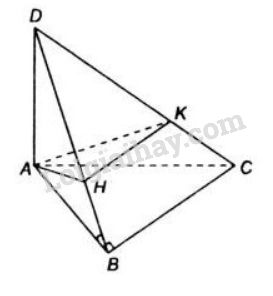
a) Tam giác ABCABC vuông tại BB nên AB⊥BCAB⊥BC (1)
AD vuông góc với (α) nên AD⊥BC (2)
Từ (1) và (2) suy ra BC⊥(ABD) suy ra BC⊥BD
(ABC)∩(DBC)=BCBD⊥BCAB⊥BC}
⇒ góc giữa hai mặt phẳng (ABC) và (DBC) là góc giữa hai đường thẳng BD và BA
Mà DA⊥(ABC)⇒DA⊥AB ⇒^ABD<900
Vậy ^ABD là góc giữa hai mặt phẳng (ABC) và (DBC).
b)
BC⊥(ABD)BC⊂(BCD)} ⇒(ABD)⊥(BCD)
c) Do (P) đi qua A,H,K nên mặt phẳng (P)≡(AHK) đi qua A và vuông góc với DB nên HK⊥BD
Trong (BCD) có: HK⊥BD và BC⊥BD nên suy ra HK//BC.
Chú ý:
Từ chứng minh trên ta có thể suy ra cách dựng (P) như sau:
Trong (DAB), qua A kẻ đường thẳng vuông góc với DB cắt DB tại H.
Trong (DBC), kẻ đường thẳng qua H và vuông góc với DB cắt DC tại K.
Từ đó ta có (P) chính là (AHK).

