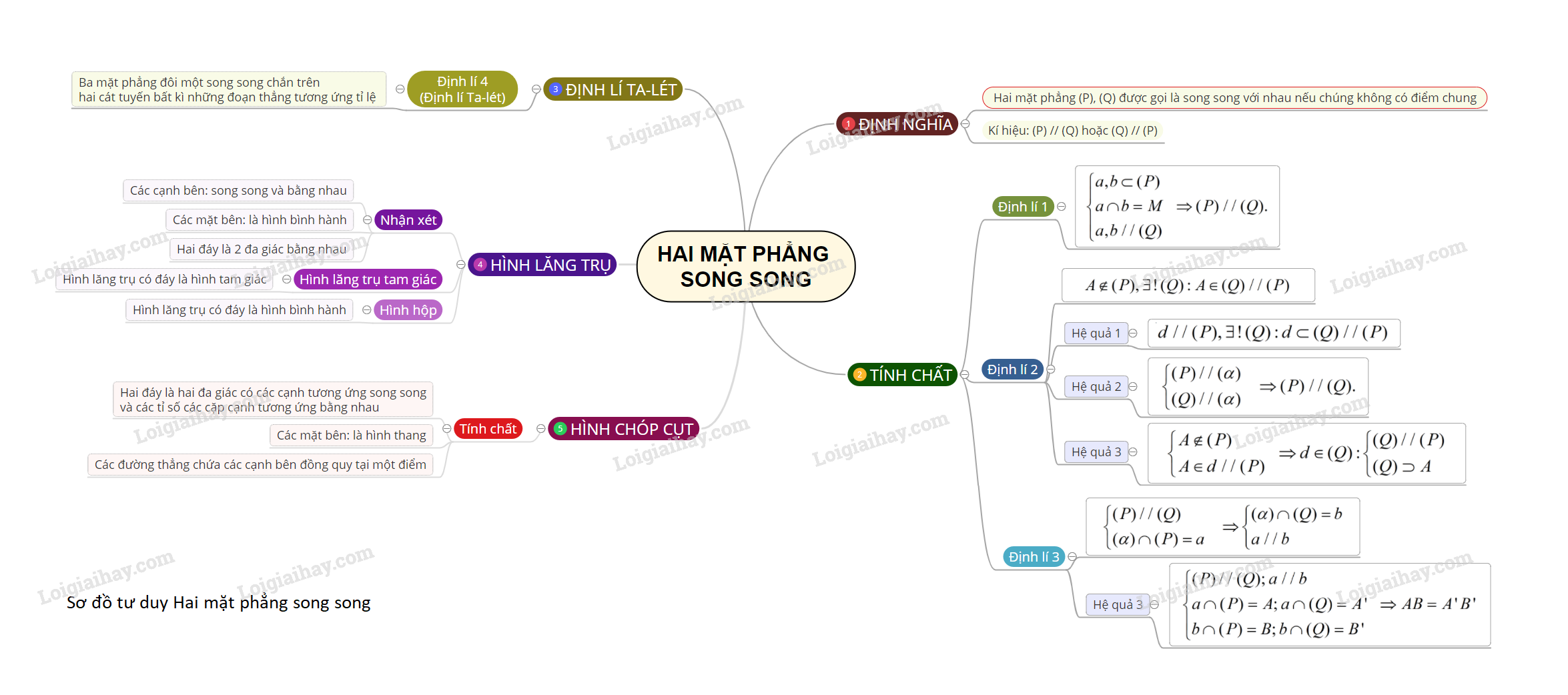
1. Đinh nghĩa:
Hai mặt phẳng gọi là song song với nhau nếu chúng không có điểm chung.
2. Tính chất:
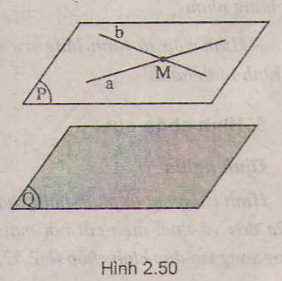
- Nếu mặt phẳng (P) chứa hai đường thẳng a và b cắt nhau và cùng song song với mặt phẳng (Q) thì (P)//(Q) 9h.2.50) ( Đây là tính chất quan trọng dùng để chứng minh hai mặt phẳng song song).
- Qua một điểm ở ngoài mặt phẳng có một và chỉ một mặt phẳng song song với mặt phẳng đó.
- Nếu đường thẳng a song song với mặt phẳng (Q) thì qua a có một và chỉ một mặt phẳng (P) song song với mặt phẳng (Q).
- Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì song song với nhau.
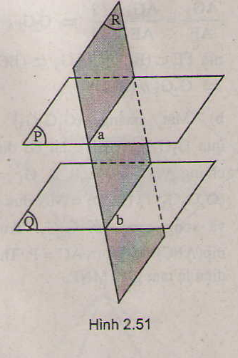
- Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau (h.2.51).
- Hai mặt phẳng song song chắn trên hai cát tuyến song song những đoạn thẳng bằng nhau.
3. Định lí Ta-lét trong không gian
Ba mặt phẳng đôi một song song chắn ra trên hai cát tuyến bất kì các đoạn thẳng tương ứng tỉ lệ.