Đề bài
Giải phương trình 2cos2x1−sin2x=02cos2x1−sin2x=0
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Tìm ĐKXĐ.
+) AB=0⇒A=0AB=0⇒A=0
+) Giải phương trình lượng giác cơ bản: cosx=cosα⇔[x=α+k2πx=−α+k2π(k∈Z)
Lời giải chi tiết
Điều kiện: sin2x≠1⇔2x≠π2+k2π ⇔x≠π4+kπ(k∈Z)
2cos2x1−sin2x=0
⇒2cos2x=0
⇔cos2x=0
⇔2x=π2+kπ
⇔x=π4+kπ2(k∈Z)
Kiểm tra ĐK:
π4+kπ2≠π4+lπ
⇔kπ2≠lπ
⇔k2≠l
⇔k≠2l
Hay k không thể nhận các giá trị chẵn.
Do đó k lẻ nên k=2m+1.
Vậy x=π4+(2m+1)π2=3π4+mπ.
Vậy phương trình có nghiệm x=3π4+mπ,m∈Z.
Chú ý: Nghiệm x=3π4+mπ cũng có thể viết thành x=−π4+nπ bằng cách đặt m=n−1.
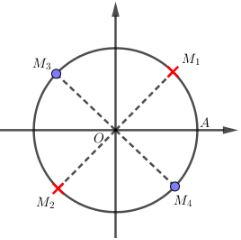
Các em cũng có thể vẽ đường tròn đơn vị để loại nghiệm như sau:
Các điểm biểu diễn x=π4+kπ là M1,M2 nhưng điều kiện là x≠π4+kπ nên hai điểm này không lấy.
Các điểm biểu diễn x=π4+kπ2 là M1,M2,M3,M4 nhưng do không lấy hai điểm M1,M2 nên các điểm biểu diễn nghiệm chỉ còn M3,M4.
Dễ thấy hai điểm này đối xứng nhau qua O và ^AOM4=−π4 nên nghiệm của phương trình là x=−π4+kπ,k∈Z.
