Đề bài
Cho hình lăng trụ tam giác ABC.A′B′C′. Gọi M và M′ lần lượt là trung điểm của các cạnh BC và B′C′
a) Chứng minh rằng AM song song với A′M′.
b) Tìm giao điểm của mặt phẳng (AB′C′) với đường thẳng A′M
c) Tìm giao tuyến d của hai mặt phẳng (AB′C′) và (BA′C′)
d) Tìm giao điểm G của đường thẳng d với mặt phẳng (AM′M). Chứng minh G là trọng tâm của tam giác AB′C′.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Chứng minh AA′M′M là hình bình hành.
b) Tìm điểm chung của mặt phẳng (AB′C′) với đường thẳng A′M
c) Tìm hai điểm chung của hai mặt phẳng (AB′C′) và (BA′C′).
d) Tìm điểm chung của đường thẳng d với mặt phẳng (AM′M), chứng minh G là giao điểm của hai đường trung tuyến của tam giác AB′C′.
Lời giải chi tiết
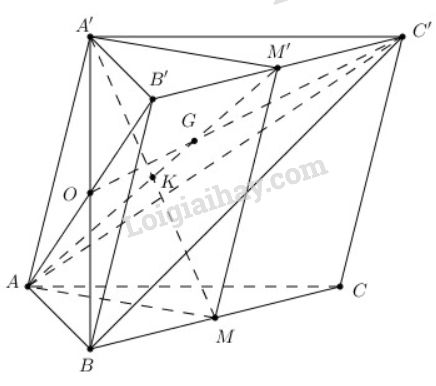
a) Xét tứ giác BMM′B′ có BM//B′M′ và BM=B′M′ nên BMM′B′ là hình bình hành.
⇒MM′//BB′//AA′ và MM′=BB′=AA′⇒AA′M′M là hình bình hành.
⇒AM//A′M′
b) Trong mp(AA′M′M), gọi K=MA′∩AM′ ⇒{K∈A′MK∈AM′⊂(AB′C′) ⇒K=A′M∩(AB′C′)
c) Trong (ABB′A′) gọi O=AB′∩A′B
⇒{O∈AB′⊂(AB′C′)O∈A′B⊂(BA′C′) ⇒O∈(AB′C′)∩(BA′C′)
Mà C′∈(AB′C′)∩(BA′C′) nên ⇒OC′=(AB′C′)∩(BA′C′).
d) Trong (AB′C′): gọi G=C′O∩AM′,
G∈AM′⊂(AMM′) nên G=d∩(AMM′).
Mà O,M′ lần lượt là trung điểm AB′ và B′C′ nên G là trọng tâm của tam giác AB′C′.

