Đề bài
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB=a,BC=b,CC′=c.
a) Tính khoảng cách từ B đến mặt phẳng (ACC′A′).
b) Tính khoảng cách giữa hai đường thẳng BB′ và AC′.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Xác định và tính khoảng cách từ điểm B đến (ACC′A′) bằng cách kẻ BH⊥AC.
Áp dụng hệ thức lượng trong tam giác vuông để tính khoảng cách vừa xác định được.
b) Xác định mặt phẳng chứa đường thẳng này và song song với đường thẳng kia. Đưa về bài toán xác định khoảng cách từ 1 điểm đến 1 mặt phẳng.
Lời giải chi tiết
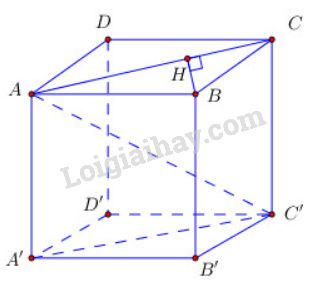
a) Trong (ABCD) kẻ BH⊥AC(H∈AC)(1)
Ta có: CC′⊥(ABCD)⇒CC′⊥BH(2)
Từ (1) và (2) suy ra BH⊥(ACC′A′).
Áp dụng hệ thức lượng trong tam giác vuông ABC ta có:
1BH2=1AB2+1BC2 =1a2+1b2=a2+b2a2b2⇒BH=ab√a2+b2
Cách khác:
Ta có:
{AA′⊥(ABCD)AA′⊂(ACC′A′)⇒(ACC′A′)⊥(ABCD){(ACC′A′)∩(ABCD)=ACBH⊂(ABCD)BH⊥AC⇒BH⊥(ACC′A′)AC=√AB2+BC2=√a2+b2BH.AC=AB.BC⇒BH=AB.BCAC=ab√a2+b2
b) Ta có: AC′⊂(ACC′A′)//BB′
⇒d(BB′,AC′)=d(BB′;(ACC′A′)=d(B,(ACC′A′))=BH.
⇒d(BB′;AC′)=ab√a2+b2

