Đề bài
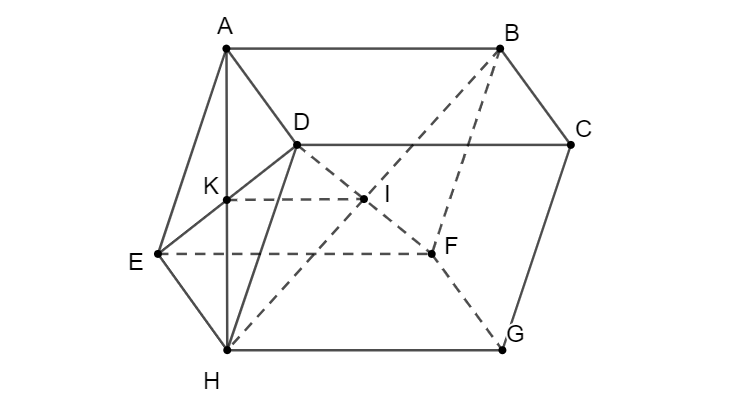
Cho hình hộp . Gọi là giao điểm của và , là giao điểm của và . Chứng minh ba véctơ , , đồng phẳng.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Chứng minh giá của các véctơ , song song với mặt phẳng chứa véctơ . Từ đó suy ra ba véctơ đồng phẳng.
Lời giải chi tiết
là giao điểm của hai đường chéo hình bình hành do đó là trung điểm của .
là giao điểm của hai đường chéo hình bình hành do đó là trung điểm của .
là đường trung bình của tam giác .
(1)
Ta có: là hình bình hành
(2)
Từ (1) và (2) suy ra: các véctơ , song song với mặt phẳng chứa véctơ
Vậy , , đồng phẳng.