Đề bài
Cho hai điểm A,B và đường tròn tâm O không có điểm chung với đường thẳng AB. Qua mỗi điểm M chạy trên đường tròn (O) dựng hình bình hành MABN. Chứng minh rằng: điểm N thuộc một đường tròn xác định.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Chứng minh N là ảnh của M qua phép tinh tiến theo vecto (→AB) cố định.
+) Xác định ảnh của M khi M chạy trên (O). Tức là tìm ảnh của (O) qua phép tịnh tiến.
Lời giải chi tiết
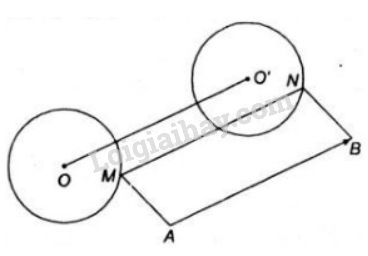
Vì MABN là hình bình hành nên →MN=→AB không đổi.
⇒T→AB(M)=N.
Gọi (O′,R) là ảnh của (O,R) qua phép tịnh tiến theo →AB, cố định.
Vì M∈(O) nên N=T→AB(M)∈T→AB((O))=(O′)
Vậy N∈(O′) (đpcm).

