Đề bài
Cho tứ diện OABCOABC có ba cạnh OA,OB,OCOA,OB,OC đôi một vuông góc. Gọi HH là chân đường vuông góc hạ từ OO tới mặt phẳng (ABC)(ABC). Chứng minh rằng:
a) H là trực tâm của tam giác ABCABC;
b) 1OH2=1OA2+1OB2+1OC2.1OH2=1OA2+1OB2+1OC2.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Chứng minh AB⊥CH;BC⊥AHAB⊥CH;BC⊥AH.
b) Sử dụng hệ thức lượng trong tam giác vuông.
Lời giải chi tiết
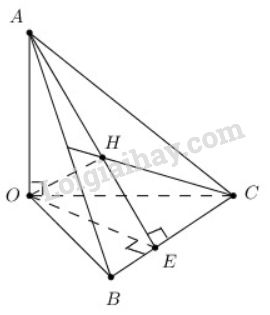
a) HH là hình chiếu của OO trên mp (ABC)(ABC) nên OH⊥(ABC)⇒OH⊥BCOH⊥(ABC)⇒OH⊥BC.
Mặt khác: OA⊥OBOA⊥OB, OA⊥OCOA⊥OC
⇒OA⊥(OBC)⇒OA⊥BC⇒OA⊥(OBC)⇒OA⊥BC
{BC⊥OHBC⊥OAOA∩OH=O ⇒BC⊥(OAH)
Mà AH⊂(OAH) ⇒BC⊥AH (1)
Ta có: {OB⊥OAOB⊥OC⇒OB⊥(OAC)
Mà AC⊂(OAC)⇒OB⊥AC
OH⊥(ABC)⇒OH⊥AC
Do đó {OB⊥ACOH⊥AC⇒AC⊥(OBH) ⇒AC⊥BH (2)
Từ (1) và (2) ta có tam giác ABC có
{AH⊥BCBH⊥ACAH∩BH=H
⇒H là trực tâm của tam giác ABC.
b) Trong mặt phẳng (ABC) gọi E=AH∩BC
{OH⊥(ABC)AE⊂(ABC)⇒OH⊥AE
Ta có: {OA⊥(OBC)OE⊂(OBC)⇒OA⊥OE ⇒ΔOAE vuông tại O có đường cao OH
⇒1OH2=1OA2+1OE2 (hệ thức giữa cạnh và đường cao trong tam giác vuông OAE)
Lại có: {BC⊥(OAH)OE⊂(OAH)⇒BC⊥OE
Mà OB⊥OC nên ΔOBC vuông tại O có OE là đường cao.
⇒1OE2=1OB2+1OC2
Vậy 1OH2=1OA2+1OE2=1OA2+1OB2+1OC2 (đpcm).
Nhận xét: Biểu thức này là mở rộng của công thức tính đường cao thuộc cạnh huyền của tam giác vuông: 1h2=1b2+1c2.

