Đề bài
Cho hình hộp \(ABCD.A'B'C'D'\). Chứng minh rằng:
a) \(\overrightarrow{AB}\) + \(\overrightarrow{B'C'}\) + \(\overrightarrow{DD'}\) = \(\overrightarrow{AC'}\);
b) \(\overrightarrow{BD}\) - \(\overrightarrow{D'D}\) - \(\overrightarrow{B'D'}\) = \(\overrightarrow{BB'}\);
c) \(\overrightarrow{AC}\) + \(\overrightarrow{BA'}\) + \(\overrightarrow{DB}\) + \(\overrightarrow{C'D}\) = \(\overrightarrow{0}\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Dựa vào các vector bằng nhau và quy tắc ba điểm.
Lời giải chi tiết
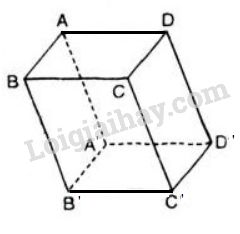
a) Ta có: \(\overrightarrow {B'C'} = \overrightarrow {BC} ;\overrightarrow {DD'} = \overrightarrow {CC'} \)
\(\overrightarrow{AB}\) + \(\overrightarrow{B'C'}\) + \(\overrightarrow{DD'}\)
= \(\overrightarrow{AB}\) + \(\overrightarrow{BC}\) + \(\overrightarrow{CC'}\)
\(= \overrightarrow {AC} + \overrightarrow {CC'} \)
= \(\overrightarrow{AC'}\);
b) \(\overrightarrow{BD}\) - \(\overrightarrow{D'D}\) - \(\overrightarrow{B'D'}\)
= \(\overrightarrow{BD}\) + \(\overrightarrow{DD'}\) + \(\overrightarrow{D'B'}\)
\( = \overrightarrow {BD'} + \overrightarrow {D'B'} \)
= \(\overrightarrow{BB'}\);
c) Ta có: \(BA'D'C\) là hình bình hành \( \Rightarrow \overrightarrow {BA'} = \overrightarrow {CD'} \)
\(BDD'B'\) là hình bình hành \( \Rightarrow \overrightarrow {DB} = \overrightarrow {D'B'} \)
\(AB'C'D\) là hình bình hành \( \Rightarrow \overrightarrow {C'D} = \overrightarrow {B'A} \)
\(\overrightarrow{AC}\) + \(\overrightarrow{BA'}\) + \(\overrightarrow{DB}\) + \(\overrightarrow{C'D}\)
= \(\overrightarrow{AC}\) + \(\overrightarrow{CD'}\) + \(\overrightarrow{D'B'}\) + \(\overrightarrow{B'A}\)
\( = \overrightarrow {AD'} + \overrightarrow {D'B'} + \overrightarrow {B'A} \)
\(= \overrightarrow {AB'} + \overrightarrow {B'A} \)
= \(\overrightarrow{0}\).

