Đề bài
Nêu cách tìm tâm vị tự của hai đường tròn.
Lời giải chi tiết
Gọi hai đường tròn là \(({I_1}{\rm{; }}{R_1})\) và \(({I_2}{\rm{; }}{R_2})\).
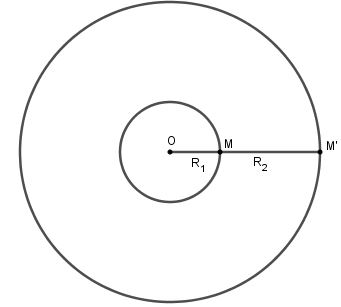
+ TH1: \({I_1}\; \equiv {\rm{ }}{I_2}\)
Khi đó tâm vị tự \(O \equiv {\rm{ }}{I_1}\; \equiv {\rm{ }}{I_2}\); tỉ số vị tự \({k_1} = \frac{{{R_2}}}{{{R_1}}}\) và \({k_2} = - \frac{{{R_2}}}{{{R_1}}}\) biến đường tròn \(({I_1}{\rm{; }}{R_1})\) thành đường tròn \(({I_2}{\rm{; }}{R_2})\).
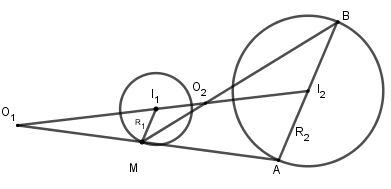
+ TH2: \({I_1}\; \ne {\rm{ }}{I_2}.\)
Vẽ bán kính \(I_1 M\) bất kì.
Dựng đường kính \(AB\) của \(({I_2}{\rm{; }}{R_2})\) sao cho \(AB // I_1M.\)
\(MA; MB\) lần lượt cắt \(I_1 I_2\) tại \(O_1\) và \(O_2\).
Khi đó \(O_1\) và \(O_2\) chính là hai tâm vị tự của hai đường tròn.